初中数学华师大版九年级上学期第23章 图形的相似 单元测试
试卷更新日期:2021-08-05 类型:单元试卷
一、单选题
-
1. 如图, 平行 平行 ,下列比例式中正确的是( )
 A、 B、 C、 D、2. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( )
A、 B、 C、 D、2. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( ) A、 B、 C、 D、3. 如图, 、 交于 点, ,则下列结论一定正确的是( )
A、 B、 C、 D、3. 如图, 、 交于 点, ,则下列结论一定正确的是( ) A、 B、 C、 D、4. 如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到 ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为( )
A、 B、 C、 D、4. 如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到 ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为( )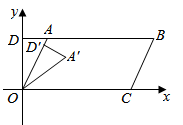 A、 B、 C、 D、5. 如图,平行四边形 的对角线 、 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( )
A、 B、 C、 D、5. 如图,平行四边形 的对角线 、 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( ) A、5.5 B、5 C、4 D、36. 如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过P点的直线交AB边于点Q,若以A,P,Q为顶点的三角形和以A,B,C为顶点的三角形相似。则AQ的长为( )
A、5.5 B、5 C、4 D、36. 如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过P点的直线交AB边于点Q,若以A,P,Q为顶点的三角形和以A,B,C为顶点的三角形相似。则AQ的长为( )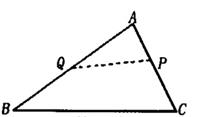 A、3 B、3或 C、3或 D、7. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )
A、3 B、3或 C、3或 D、7. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )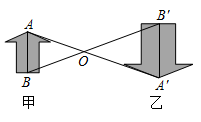 A、8 B、9 C、10 D、158. 如图,A , B的坐标为(2,0),(0,1),若将线段AB平移至A1B1 , 点A对应点A1(3,b),点B对应点B1(a , 3),则a+b的值为( )
A、8 B、9 C、10 D、158. 如图,A , B的坐标为(2,0),(0,1),若将线段AB平移至A1B1 , 点A对应点A1(3,b),点B对应点B1(a , 3),则a+b的值为( )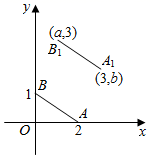 A、-1 B、1 C、3 D、59. 如图, 在平面直角坐标系中, 的顶点 与原点重合,点 在 轴的正半轴上, 按以下步骤作图:①以点 为圆心,适当长度为半径作 弧,分别交边 , 于点 , ;②分别以点 , 为圆心,大于 的长为半径作弧, 两弧在 内交于点 ;③作射线 ,交边 于点 .若 , ,则点 的坐标为( )
A、-1 B、1 C、3 D、59. 如图, 在平面直角坐标系中, 的顶点 与原点重合,点 在 轴的正半轴上, 按以下步骤作图:①以点 为圆心,适当长度为半径作 弧,分别交边 , 于点 , ;②分别以点 , 为圆心,大于 的长为半径作弧, 两弧在 内交于点 ;③作射线 ,交边 于点 .若 , ,则点 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为.11. 如图,在 中,点 分别在边 上,且 , 与四边形 的面积的比为.
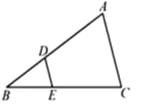 12. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
12. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .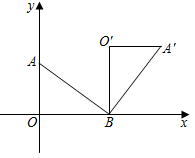 13. 在等腰梯形ABCD中,AD∥BC , ∠B=∠C=30°,AD的长为3,高AH的长为 ,那么梯形的中位线长为 .
13. 在等腰梯形ABCD中,AD∥BC , ∠B=∠C=30°,AD的长为3,高AH的长为 ,那么梯形的中位线长为 . 14. 如图,正方形ABCD中,点E是CD边上一点,连结BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连结AF,有以下五个结论:① ;② ;③ ;④ ;⑤若 ,则 ,你认为其中正确是(填写序号)
14. 如图,正方形ABCD中,点E是CD边上一点,连结BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连结AF,有以下五个结论:① ;② ;③ ;④ ;⑤若 ,则 ,你认为其中正确是(填写序号)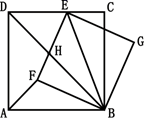
三、解答题
-
15. 如图,利用标杆 测量楼高,点A,D,B在同一直线上, , ,垂足分别为E,C.若测得 , , ,楼高 是多少?
 16. 如图,在直角三角形 中, ,作 的内接矩形 .设 ,求x取何值时矩形的面积最大?
16. 如图,在直角三角形 中, ,作 的内接矩形 .设 ,求x取何值时矩形的面积最大?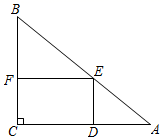 17. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.
17. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.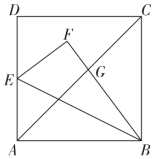
四、作图题
-
18. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标是A(0,﹣2),B(6,﹣4),C(2,﹣6).
 (1)、请画出与△ABC关于x轴对称的△A1B1C1 .(2)、以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴左侧画出△A2B2C2 .(3)、在y轴上存在点P,使得△OB2P的面积为6,请直接写出满足条件的点P的坐标.
(1)、请画出与△ABC关于x轴对称的△A1B1C1 .(2)、以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴左侧画出△A2B2C2 .(3)、在y轴上存在点P,使得△OB2P的面积为6,请直接写出满足条件的点P的坐标.五、综合题
-
19. 如图


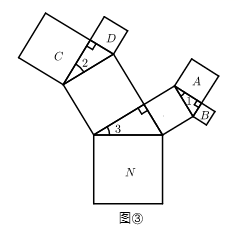 (1)、阅读理解:我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理和推理过程;(2)、问题解决:勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形 的中心 ,作 ,将它分成4份.所分成的四部分和以 为边的正方形恰好能拼成以 为边的正方形.若 ,求 的值;(3)、拓展探究:如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形 的边长为定值 ,小正方形 的边长分别为 .已知 ,当角 变化时,探究 与 的关系式,并写出该关系式及解答过程( 与 的关系式用含 的式子表示).
(1)、阅读理解:我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理和推理过程;(2)、问题解决:勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形 的中心 ,作 ,将它分成4份.所分成的四部分和以 为边的正方形恰好能拼成以 为边的正方形.若 ,求 的值;(3)、拓展探究:如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形 的边长为定值 ,小正方形 的边长分别为 .已知 ,当角 变化时,探究 与 的关系式,并写出该关系式及解答过程( 与 的关系式用含 的式子表示).
-