浙江省金华市浦江县2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-05 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题2分，共20分）

1. 如图，梯子的各条横档互相平行，若∠2＝80°，那么∠1＝（）

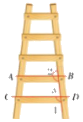A、80° B、100° C、60° D、120°

查看试题解析
2. 已知二元一次方程4x﹣7y＝3．用x的代数式表示y ，正确的是（）

A、 $\frac{3 - 7 y}{4}$ B、 $\frac{3 + 7 y}{4}$ C、 $\frac{4 x - 3}{7}$ D、 $\frac{4 x + 3}{7}$

查看试题解析
3. 计算[（﹣x）³]²＝（）

A、﹣x⁶ B、x⁶ C、﹣x⁵ D、x⁵

查看试题解析
4. 如果（x﹣4）（x+3）＝x²+mx﹣12，则m的值为（）

A、1 B、﹣1 C、7 D、﹣7

查看试题解析
5. 下列命题中，真命题有（）个
（1）同角的补角相等．（2）一条直线截另外两条直线所得的同位角相等．（3）有公共顶点且相等的两个角是对顶角．（4）两个无理数的和仍是无理数．

A、1 B、2 C、3 D、4

查看试题解析

6. 如图是小聪同学的作业，在※处填的理由是（）

如图，∠A+∠D＝180°，则∠DCE＝∠B ．完成下面的说理过程．

解：已知∠A+∠D＝180°，根据（同旁内角互补，两直线平行），得AB∥CD

又根据（※）得∠DCE＝∠B ．

A、两直线平行，同位角相等 B、两直线平行，内错角相等 C、两直线平行，同旁内角互补 D、同位角相等，两直线平行

查看试题解析

7. 已知b﹣ $\frac{1}{2}$ a²＝0，则 $\frac{3 a b + 3 b}{a^{2} + b}$ 的值为（）

A、a²+1 B、b²+1 C、a+1 D、b+1

查看试题解析
8. 根据如图信息，某摩托车厂去年第四季度比第三季度的产量增加了约（）

A、40.2% B、29.6% C、43.3% D、67.3%

查看试题解析
9. 关于x的分式方程 $\frac{x - 2}{x - 4}$ ＝ $\frac{m^{2}}{2 x - 8}$ 有增根，则m的值为（）

A、1 B、±1 C、2 D、±2

查看试题解析
10. 如图是将正方形ABCD和正方形CEFG拼在一起的图形，点B ， C ， E在同一条直线上，连结BD ， BF ．若阴影部分△BDF的面积为8，则正方形ABCD的边长为（）

A、2 B、3 C、4 D、6

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

11. 因式分解：a²﹣25＝．

查看试题解析
12. 已知 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ 是方程mx+3y=1的一个解，则m的值是．

查看试题解析
13. 一副三角板，按如图所示叠放在一起，则图中∠α的度数是 °．

查看试题解析
14. 如图，直线l₁∥l₂ ， AB⊥l₁ ，垂足为C ， BD与l₂相交于点E ，若∠α＝20°，则∠B＝°．

查看试题解析
15. 一项工作由甲单独做，需a天完成；如果由甲、乙两人合作，则可提前2天完成，则乙单独完成该项工作需要的天数为天．

查看试题解析
16. 斜边与正方形ABCD边重合的四个全等的直角三角形图形如图所示放置，拼出了面积为4cm²的小正方形EFGH ，且小正方形的顶点刚好为每个直角三角形一条直角边的中点．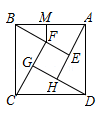

(1)、正方形ABCD的面积为 cm² ．

(2)、点F到线段AB的距离FM＝cm ．

查看试题解析

三、解答题（本题有8小题，每题都要写出必要的解答过程,共62分）

17. 计算：

(1)、a²÷a³•（﹣3a）²；

(2)、（8x²﹣12x³+16x）÷4x ．

查看试题解析
18. 解方程组：

(1)、 ${\begin{matrix} 5 x = 3 y \\ x - y = 4 \end{matrix}$ ；

(2)、 ${\begin{matrix} 2 m + 7 n = 5 \\ 3 m + n = - 2 \end{matrix}$ ．

查看试题解析
19. 解分式方程：

(1)、 $\frac{x - 3}{2 x + 1}$ ＝ $\frac{1}{9}$ ；

(2)、 $\frac{2 + x}{2 - x}$ + $\frac{15}{x^{2} - 4}$ ＝﹣1．

查看试题解析
20. 如图，已知AB∥CD ， AD∥BE ，点C在线段BE上，∠BAE＝87°，∠E＝20°，AE与CD交于点F ．

(1)、求∠ADC的度数；

(2)、连结BF ，若∠AFB：∠BFC＝1：2，求∠FBC的度数．

查看试题解析
21. 对若干只电灯泡的使用寿命进行检测，得到如图的频数分布直方图（每一组含前一个边界值，不含后一个边界值）．请根据这个直方图回答下列问题．

(1)、被检测的电灯泡共有多少只？

(2)、直方图中的组距为多少？

(3)、使用寿命在550小时以上（含550小时）的灯泡有多少只？占被检测灯泡总数的百分之几？

查看试题解析
22. 如图，在△ABC和△DEF中，B ， E ， C ， F在同一条直线上，下列给出四个论断：
①AB＝DE；②AC＝DF；③∠ACB＝∠DFE；④BE＝CF ．解答下列问题：

(1)、任选三个作为已知条件，余下一个作为结论，得到一个真命题．（填入下列横线上）
条件：，结论：．（填序号即可）

(2)、证明（1）中你选的命题．

(3)、若△DEF是由△ABC沿BC方向平移得到的，已知△ABC的周长为m ，则平移距离AD＝时，四边形ABFD的周长是△ABC周长的两倍．

查看试题解析
23. 疫情防控期间，某班级购买一批消毒液供学生使用，有甲，乙两种不同消毒液供选择．已知甲种消毒液比乙种消毒液每瓶贵3元，用360元单独购买其中一种消毒液时，可以比单独购买另一种消毒液多6瓶．

(1)、问甲，乙两种消毒液的单价是多少？

(2)、若用360元（钱用完）购买两种消毒液，且甲种消毒液不少于16瓶，问有几种购买方案（两种消毒液都要有）？请通过计算说明．

查看试题解析
24. 已知∠MON＝48°，点C是∠MON的平分线上一动点，点A ， B分别是边ON ， OM上动点，AB交OC于点D ．

(1)、如图1，当AB⊥OC ， AC∥OB时，图中有对全等的三角形，∠DAC＝°．

(2)、如图2，当AB平分∠OAC ，且∠DAC＝∠DCA时，求∠OBA的度数．

(3)、如图3，当BA⊥AN于点A ，在点C移动过程中，△ACD内有两个角相等时，求∠OAC的度数．

查看试题解析

四、选择题：（本题有两小题，每小题2分，共4分）

25. 现有价格相同的6种不同商品，从今天开始每天分别降价10%或涨价10%，若干天后，这6种商品的价格互不相同，设最高价格和最低价格的比值为r ，则r的最小值为（）

A、（ $\frac{11}{9}$ ）³ B、（ $\frac{11}{9}$ ）⁴ C、（ $\frac{11}{9}$ ）⁵ D、（ $\frac{11}{9}$ ）⁶

查看试题解析
26. 如图，AD∥BE ， AC与BC相交于点C ，且∠1＝ $\frac{1}{n}$ ∠DAB ， ∠2＝ $\frac{1}{n}$ ∠EBA ．若∠C＝45°，则n＝（）

A、2 B、3 C、4 D、5

查看试题解析

五、填空题：（本题有两小题，每小题3分，共6分）

27. 若3x²+kx+4被3x﹣1除后余2，则k的值为．

查看试题解析
28. 已知 $\frac{x}{x^{2} - x + 1}$ ＝ $\frac{1}{7}$ ，则 $\frac{x^{2}}{x^{4} - x^{2} + 1}$ ＝．

查看试题解析

六、解答题：（本题有两小题，每小题5分，共10分）

29. 如图，在△ABC中，∠BAC＝90°，AB＝6，AC＝8，BC＝10，若AD平分∠BAC交BC于点D ，求BD的长．

查看试题解析
30. 某工厂的一条流水线匀速生产出产品，在有一些产品积压的情况下，经过试验，若安排9人包装，则5小时可以包装完所有产品；若安排6人包装，则需要10小时才能包装完所有产品．假设每个人的包装速度一样，现要在2小时内完成产品包装的任务，问至少需要安排多少人？

查看试题解析