浙江省绍兴市上虞区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-05 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分.）

1. 二元一次方程2x+y =7中，若x=2，则y的值是（ ).

A、3 B、11 C、-3 D、-11

查看试题解析
2. 在5×5的方格中，将图1中的图形N经平移后的位置如图2所示，则下列关于图形N的平移方法中，正确的是（）.

A、向下移动2格 B、向下移动3格 C、向上移动2格 D、向上移动3格

查看试题解析
3. 要使分式 $\frac{2 x - 4}{x - 1}$ 有意义，x的取值应满足（）

A、x≠2 B、x=2 C、x≠1 D、x=1

查看试题解析
4. 下列运算正确的是（ ) .

A、 $a^{3} - a^{2} = a$ B、 ${(a^{3})}^{2} = a^{5}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{3} \div a^{2} = a$

查看试题解析
5. 如图，将一条两边沿互相平行的纸带折叠.设∠1为x度，用关于x的代数式表示α，则表示正确的是（）.

A、 $α = 120^{\circ} - \frac{1}{2} x$ B、 $α = 90^{\circ} - \frac{1}{2} x$ C、 $α = 60^{\circ} + \frac{1}{2} x$ D、 $α = 45^{\circ} + \frac{1}{2} x$

查看试题解析
6. 小敏玩“抖空竹”游戏，她发现可以将某一时刻的情形抽象成数学问题：如图，已知AB //CD，∠BAE=82°，∠DCE=115°，则∠E的度数是（ ) .

A、31° B、32° C、33° D、34°

查看试题解析
7. 某防护用品厂计划生产240000个口罩，但在实际生产时，__?_.求实际每天生产口罩的个数，在这个问题中，若设实际每天生产口罩x个，由题意可列出的方程为 $\frac{240000}{x - 200} - \frac{240000}{x} = 10$ 则问题中用“__?_”所表示的条件应该是（）

A、每天比原计划多生产200个，结果延期10天完成 B、每天比原计划少生产200个，结果提前10天完成 C、每天比原计划少生产200个，结果延期10天完成 D、每天比原计划多生产200个，结果提前10天完成

查看试题解析
8. 下列多项式能用公式法分解因式的是( ）.
$① - 4 x^{2} - y^{2} ② 4 x^{2} - {(- y)}^{2} ③ a^{2} + 2 a b - b^{2} ；$ ④ $x + 1 + \frac{x^{2}}{4}$ ⑤ $m^{2} n^{2} + 4 - 4 m n$

A、①③④⑤ B、②③④ C、②④⑤ D、②③④⑤

查看试题解析
9. 将图1中四个阴影小正方形拼成边长为2所示，根据两个图形中阴影部分面积间的关系，可以验证下列哪个乘法公式（）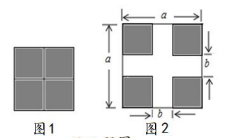

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 ${(a + b)}^{2} = {(a - b)}^{2} + 4 a b$

查看试题解析
10. 如图，在△ABC中，AB＝12，点D，E分别在边AC，AB上，将△ADE沿直线DE折叠，使点A落在点F处，将线段EF向右平移，平移后恰能与边BC重合，连结CF.若2BC-CF＝15，则BC＋2CF的值为（）.

A、12 B、15 C、18 D、20

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分.）

11. 若分式 $\frac{x - 1}{x + 2}$ 的值为0，则x=。

查看试题解析
12. 解二元一次方程组 ${\begin{matrix} x + y = 2 \\ x - y = 5 \end{matrix}$ 时，为便捷求出末知数y的值，宜采用法消元.

查看试题解析
13. 第七次全国人口普查属于（填“全面”或“抽样”）调查．

查看试题解析
14. 如图，将直角三角板ABC与直尺贴在一起，使三角板ABC的直角顶点C在直尺的一边上，若∠1＝63°，则∠2的度数为．

查看试题解析
15. 如图，点A，B在数轴上所对应的数分别为-2和 $\frac{x}{x + 3}$ 且点A，B到原点的距离相等，则.

查看试题解析
16. 已知二元一次方程组 ${\begin{matrix} 2 x - 3 y = 13 \\ 3 x + 5 y = 30.9 \end{matrix}$ 的解为 ${\begin{matrix} x = 8.3 \\ y = 1.2 \end{matrix}$ ，则方程组 ${\begin{matrix} 2 (x + y) - 3 (x - y) = 13 \\ 3 (x + y) + 5 (x - y) = 30.9 \end{matrix}$ 的解为.

查看试题解析
17. 我国古代问题：以绳测井，若将绳三折测之，绳多四尺，若将绳四折测之，绳多一尺，井深几何？这段话的意思是：用绳子量井深，把绳三折来量，井外余绳四尺，把绳四折来量，井外余绳一尺.井深几尺？你得到的答案：井深是尺．

查看试题解析
18. 如图，在一个大长方形中放入六个形状、大小相同的小长方形，有关尺寸如图所示，则图中大长方形ABCD的面积是cm²

查看试题解析

三、解答题（本题共有6小题，共46分.）

19. 解答下列各题：

(1)、解分式方程： $\frac{3}{1 - y} = \frac{y}{y - 1} - 5$

(2)、先化简，再求值：(2a−3)(3a+1)−6a(a−4)，其中 $a = \frac{2}{17}$

查看试题解析
20. 因式分解：

(1)、 $4 x^{2} - y^{2}$

(2)、
9a³-6a²b+ab²

查看试题解析
21. 为庆祝中国共产党百年华诞，某校德育处组织开展以“红色经典伴我成长”为主题的系列教育活动.为了解该校学生本学期阅读革命红书册数的情况，随机抽取若干学生进行调查，得到如下不完整的统计图表.

根据图中信息，解答下列问题：

(1)、这次调查共抽取学生人；m＝， n＝.

(2)、请将条形统计图补充完整；

(3)、若该校共有学生1200人，根据调查结果，请你估计该校学生本学期阅读革命红书册数4册及以上的学生人数．

查看试题解析
22. 在学了乘法公式“(a±b)²= a²±2ab+b²”的应用后，王老师提出问题：求代数式x²＋4x＋5的最小值.要求同学们运用所学知识进行解答.
同学们经过探索、交流和讨论，最后总结出如下解答方法：

解：x²＋4x＋5=x²＋4x+2²-2²+5=(x+2)²+1，

∵(x+2)²≥0，".(x+2)²+1≥1.

当(x+2)²=0时，(x+2)²+1的值最小，最小值是1

∴x²+4x＋5的最小值是1.

请你根据上述方法，解答下列各题：

(1)、直接写出(x-1)²+3的最小值为

(2)、求代数式x²＋10x＋32的最小值.

(3)、若7x-x²+y-11=0，求x＋y的最小值.

查看试题解析
23. 随着5G网络技术的快速发展，市场对5G产品的需求越来越大.某5G产品生产厂家承接了27000个电子元件的生产任务，计划安排甲、乙两个车间共50名工人，合作生产20天完成．已知甲车间每人每天生产25个，乙车间每人每天生产30个．

(1)、求甲、乙两个车间各有多少名工人将参与生产？

(2)、为提前完成生产任务，该厂家设计了两种生产方案：方案1：甲车间租用先进生产设备，工人的工作效率可提高20%，乙车间维持不变；方案2：乙车间再临时招聘若干名工人（工作效率与原工人相同），甲车间维持不变．若设计的这两种生产方案，厂家完成生产任务的时间相同，求乙车间需要临时招聘的工人数.

查看试题解析
24. 我区防汛指挥部在一河道的危险地带两岸各安置一探照灯，便于夜间查看江水及两岸河堤的情况．如图1，灯A光射线自AM顺时针旋转至AN便立即逆时针旋转至AM，如此循环.灯B光射线自BP顺时针旋转至BQ便立即逆时针旋转至BP，如此循环.两灯交叉照射且不间断巡视．若灯A转动的速度是a度/秒，灯B转动的速度是b度/秒，且a，b满足(a﹣4b)²+(a+b﹣5)²＝0．若这一带江水两岸河堤相互平行，即PQ∥MN，且∠BAN＝60°．根据相关信息，解答下列问题.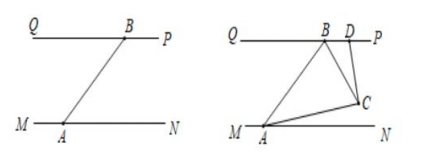

(1)、a= ， b=.

(2)、若灯B的光射线先转动24秒，灯A的光射线才开始转动，在灯B的光射线到达BQ之前，灯A转动几秒，两灯的光射线互相平行？

(3)、如图2，若两灯同时开始转动照射，在灯A的光射线到达AN之前，若两灯射出的光射线交于点C，过点C作CD⊥AC交PQ于点D，则在转动的过程中，∠BAC与∠BCD间的数量关系是否发生变化？若不变，请求出这两角间的数量关系；若改变，请求出各角的取值范围．

查看试题解析