浙江省绍兴市上虞区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-05 类型：期末考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分．）

1. 当x=0时，二次根式 $\sqrt{4 + 2 x}$ 的值等于（）

A、4 B、2 C、2 D、0

查看试题解析
2. 四个一元二次方程：①x²−2x−3=0；②x²−2x+1=0；③x²−2x+2=0；④x²=0．其中没有实数根的方程的序号是（）．

A、① B、② C、③ D、④

查看试题解析
3. 如图，在矩形ABCD中，对角线AC，BD交于点O，若△AOB的面积为2，则矩形ABCD的面积为（）．

A、4 B、6 C、8 D、10

查看试题解析
4. 一个四边形四个内角的度数之比为1：1：0.6：1，则该四边形最小内角的度数为（）．

A、75° B、70° C、65° D、60°

查看试题解析
5. 如图，在菱形ABCD中，∠B=60°，对角线AC=3，则该菱形的周长为（）．

A、12 B、15 C、6+4 $\sqrt{3}$ D、3+6 $\sqrt{3}$

查看试题解析
6. 已知反比例函数 $y = - \frac{12}{x}$ ，当 $y \leq \frac{4}{3}$ 且 $y \neq 0$ 时，自变量x的取值范围为（）．

A、 $x < 0$ B、 $x \leq - 9$ C、 $- 9 \leq x < 0$ D、 $x \leq - 9$ 或 $x > 0$

查看试题解析
7. 小敏将图1所示七巧板的其中几块，拼成如图2所示的一个四边形，则该四边形的最长边长与最短边长之比为（）．

A、2 B、3 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
8. 取一张长与宽之比为5：2的长方形纸板，剪去四个边长为5cm的小正方形（如图），并用它做一个无盖的长方体形状的包装盒．要使包装盒的容积为200cm³(纸板的厚度略去不计)，问这张长方形纸板的长与宽分别为多少厘米?
若设这张长方形纸板的长为5x厘米，则由题意可列出的方程是（）

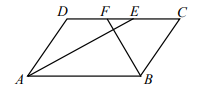
A、5(5x+10)(2x-10)=200 B、5(5x+10)(2x+10)=200 C、5(5x-10)(2x-10)=200 D、5(5x-10)(2x+10)=200

查看试题解析
9. 如图，在平行四边形ABCD中，对角线AC，BD交于点E，AC⊥BC，点F是BE的中点，连结CF．若BC=4，CF=2.5，则AB的长为（）．

A、2 $\sqrt{13}$ B、6 C、8 D、10

查看试题解析
10. 将一张长为8，宽为4的矩形纸片按如下方式进行操作：
（1）如图1，将矩形纸片折叠，使顶点B与D重合，折痕为AC，然后展开恢复原状；（2）沿着图1中虚线段AC，BD，AB，CD剪开，得到①、②、③、④四个三角形；（3）将图1中的①、②、③、④这四个三角形拼成如图2的四边形EFGH．

则四边形MNPQ的面积为（）．

A、32 B、25 C、7 D、5

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分）

11. 二次根式 $\sqrt{a - 1}$ 中，字母a的取值范围是。

查看试题解析
12. 若坐标为(−1， $\sqrt{3}$ )的点P在反比例函数 $y = \frac{k}{x}$ (k≠0，且k为常数)的图象上，则k=。

查看试题解析
13. 若x=1是一元二次方程x²-2x-m=0的一个根，则m =

查看试题解析
14. 已知一个多边形的内角和为1800°，则这个多边形的边数是。

查看试题解析
15. 如图，在 $▱$ ABCD中，AB＝8，AD＝5，∠DAB，∠ABC的平分线分别交边CD于点E，F，则EF的长为。

查看试题解析

16. 教材中有一道题：

9，如图、在反比例函数 $y = \frac{2}{x} (x > 0)$ 的图象上，有点P₁ ， P₂ ， P₃ ， P₄ ，它们的横坐标依次为1，2，3，4.分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S₁ ， S₂ ， S₃.

则S₁+S₂+S₃=（）

请你仔细审题后认真解答．你所得到的答案是。

查看试题解析

17. 如图，矩形ABCD的对角线AC，BD交于点O，AB=6，BC=8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为.

查看试题解析
18. 已知直线 $y = \frac{\sqrt{3}}{3} x + \sqrt{3}$ 与x轴，y轴分别交于点A，B，点C是射线AB上的动点，点D在第一象限，四边形0ACD是平行四边形.若点D关于直线OC的对称点D'恰好落在y轴上，则点C的坐标为。

查看试题解析

三、解答题（本大题有6小题，共46分．)

19. 解答下列各题：

(1)、计算： $\frac{1}{2} \sqrt{24} - 2 \sqrt{3} \times \sqrt{2} + \sqrt{48} \div \sqrt{2}$

(2)、设实数 $\sqrt{7}$ 的整数部分为a，小数部分为b，求(2a+b)(2a-b)的值.

查看试题解析
20. 解答下列各题：

(1)、用配方法解方程：x²+12x=-9

(2)、设x₁ ， x₂是一元二次方程5x²-9x-2=0的两根，求 $x_{1}^{2} + x_{2}^{2}$ 的值.

查看试题解析
21. 为庆祝中国共产党百年华诞，某校德育处组织开展以“红色经典伴我成长”为主题的系列教育活动．学校要求每名同学至少购买革命红书1册并进行阅读．小敏调查了班级里40名同学本学期购买革命红书册数的情况，并将结果绘制成如下统计图．请根据图中信息，解答下列问题．

(1)、这次调查获取的样本数据的众数是；中位数是．

(2)、该校共有学生1200人，根据样本数据，估计本学期学生购买革命红书4册及以上的学生共有多少人．

查看试题解析
22. 某花圃用花盆培育某种花苗，经过试验发现，每盆花的盈利与每盆株数构成一定的关系．每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆每增加1株，平均单株盈利就减少0.5元．要使每盆的盈利为10元，则每盆应植多少株?

查看试题解析
23. 如图，在平面直角坐标系中，点A，B分别是y轴和x轴的正半轴上的动
点，正方形ABCD的顶点C，D在第一象限.

(1)、当AB=2，∠OAB= 30°时，正方形ABCD的一个顶点恰好在反比例函数 $y = \frac{k}{x}$ (k为常数，x>0）的图象上，求k的值.

(2)、保持AB=2不变，移动点A，B，使0A：0B=1 ：2，求此时点D的坐标，并判断点D是否在（1）中的反比例函数图象上.

查看试题解析
24. 如图1，在矩形ABCD中，AB=4，BC=3，点E为边CD上一动点，连结AE，作点D关于直线AE的对称点F，连结EF，DF，CF，AF，DF与AE交于点G．

(1)、若DE=2，求证：AE//CF．

(2)、如图2，连结AC，BD，若点F在矩形ABCD的对角线上，求所有满足条件的DE的长．

(3)、如图3，连结BF，当点F到矩形ABCD一个顶点的距离等于2时，请直接写出△BCF的面积．

查看试题解析