浙江省杭州市淳安县等七县区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-05 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，∠B的同位角是（）

A、∠1 B、∠2 C、∠3 D、∠4

查看试题解析
2. 3^-2=（）

A、 $\frac{1}{9}$ B、- $\frac{1}{9}$ C、-6 D、 $\frac{1}{6}$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{3} + a^{3} = 2 a^{6}$ B、 ${(- a^{2})}^{3} = a^{6}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 $a^{5} \cdot a^{3} = a^{8}$

查看试题解析
4. 为了调查某校学生的身高情况，在全校的1000名学生中随机抽取了80名学生，下列说法正确的是（）

A、此次调查属于全面调查 B、样本容量是80 C、1000名学生是总体 D、被抽取的每一名学生称为个体

查看试题解析
5. 下列各式从左到右的变形属于因式分解的是（）

A、 $6 x^{2} y^{3} = 2 x^{2} \cdot 3 y^{3}$ B、 $x^{2} - 9 = (x - 3) (x + 3)$ C、 $x^{2} + 2 x + 1 = x (x^{2} + 2) + 1$ D、（x+2）（x﹣3）＝x²﹣x﹣6

查看试题解析
6. 若x≠y，则下列分式化简中，正确的是（）

A、 $\frac{x + 2}{y + 2} = \frac{x}{y}$ B、 $\frac{x - 2}{y - 2} = \frac{x}{y}$ C、 $\frac{3 x}{3 y} = \frac{x}{y}$ D、 $\frac{x^{2}}{y^{2}} = \frac{x}{y}$

查看试题解析
7. 如图是一所楼房的平面图，下列式子中不能表示它的面积的是（）

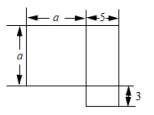A、a²+5a+15 B、（a+5）（a+3）﹣3a C、a（a+5）+15 D、a（a+3）+a²

查看试题解析
8. 已知分式 $\frac{5 x + n}{x - m}$ （m，n为常数）满足下列表格中的信息：则下列结论中错误的是（）

x的取值

－2

2

p

q

分式的值

无意义

2

0

1

A、m＝－2 B、n＝－2 C、 $p = \frac{2}{5}$ D、q＝－1

查看试题解析
9. 如图，下列条件中能判断AD∥BC的是（）
①∠1=∠2 ②∠3=∠4 ③∠2+∠5=∠6 ④∠DAB+∠2+∠3=180°

A、①③④ B、①②④ C、①③ D、①②③④

查看试题解析
10. 某超市以同样的价格卖出同样的牙刷和牙膏，以下是4天的记录：第1天，卖出13支牙刷和7盒牙膏，收入144元；第2天，卖出18支牙刷和11盒牙膏，收入219元；第3天，卖出23支牙刷和20盒牙膏，收入368元；第4天，卖出17支牙刷和11盒牙膏，收入216元，聪明的小方发现这四天中有一天的记录有误，其中记录有误的是（）

A、第1天 B、第2天 C、第3天 D、第4天

查看试题解析

二、填空题（每题4分，共24分）

11. 若使分式 $\frac{x}{x - 2}$ 有意义，则x的取值范围是.

查看试题解析
12. 一次数学测试后，某班40名学生按成绩分成5组，第1、2、3、5组的频数分别为12、9、7、8，则第4组的频率为.

查看试题解析
13. 如图，将长为a cm(a>2)，宽为b cm(b>1)的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为cm² ． (用含a、b的代数式表示，结果要求化成最简)

查看试题解析
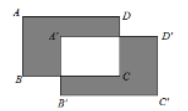14. 若4^x＝a，8^y＝b，则2^2x-3y可表示为(用含a、b的代数式表示)．

查看试题解析
15. 若 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 9 \\ b x + c y = 2 \end{array}$ 的解，则a与c的关系是.

查看试题解析
16. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S₁；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S₂ ．若a+b＝8，ab＝10，则S₁+S₂=；当S₁+S₂＝40时，则图3中阴影部分的面积S₃=.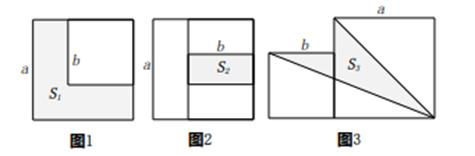

查看试题解析

三、解答题（共66分）

17. 因式分解：

(1)、a²-2ab+b²

(2)、8-2x²

查看试题解析
18. 解下列方程组或方程

(1)、 ${\begin{array}{l} 3 x + 4 y = 21 \\ x - 4 y = 7 \end{array}$

(2)、 $\frac{x}{x - 1} - 3 = \frac{2}{x - 1}$

查看试题解析

19. 某校组织全校2000名学生进行了“学史明理”问卷测试．为了解成绩的分布情况，随机抽取了部分学生的成绩（得分取整数．满分为100分），并绘制了频数分布表和频数分布直方图（不完整）．

分组	50.5≤x＜60.5	60.5≤x＜70.5	70.5≤x＜80.5	80.5≤x＜90.5	90.5≤x＜100.5	合计
频数	20	48	a	104	148	400

根据所给信息，回答下列问题：

(1)、频数分布表中，a＝．

(2)、补全频数分布直方图；

(3)、学校将对分数x在90.5≤x＜100.5范围内的学生进行奖励，请你估算出全校获奖学生的人数．

查看试题解析

20.

(1)、化简：（a＋2）(a－2)－(a－1)²

(2)、先化简 $\frac{2}{a - 1} + \frac{a^{2} - 4 a + 4}{a^{2} - 1} \div \frac{a - 2}{a + 1}$ ，再从1，－1，－2，2四个数字中选取一个合适的数作为a代入求值。

查看试题解析
21. （我国古代算题）马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两.问：

(1)、马牛各价几何？

(2)、马一十三匹、牛十头，共价几何？

查看试题解析
22. 如图

如图①，将一张长方形纸片沿EF对折，使AB落在A´B´的位置；

(1)、若∠1的度数为a，试求∠2的度数（用含a的代数式表示）；

(2)、如图②，再将纸片沿GH对折，使得CD落在C´D´的位置. ①若EF∥C´G，∠1的度数为a，试求∠3的度数（用含a的代数式表示）； ②若B´F⊥C´G，∠3的度数比∠1的度数大20°，试计算∠1的度数.

查看试题解析
23. 某商店3月份购进一批T恤衫，进价合计12万元，因畅销，商店又于4月份购进一批同品牌的T恤衫，进价为15万元，数量是3月份的1.2倍，但每件涨了5元。

(1)、求3月份购进的T恤衫的单价是多少？4月份购进了多少件T恤衫？

(2)、这两批T恤衫开始都以每件180元出售，结果4月份后期出现的出现滞销，还有一半的T恤衫没有售出，于是5月份商店便以定价的n折开始销售（1≤n≤9的正整数），结果第二批T恤衫的共盈利800m元（m为正整数），求相应n、m值．

查看试题解析

x的取值	－2	2	p	q
分式的值	无意义	2	0	1