湖南省邵阳市邵东市2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 如下字体的四个汉字中，可以看作是轴对称图形的是（）

A、 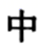B、 C、 D、

查看试题解析
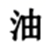2. 如图，已知∠1=65°，如果CD∥BE，那么∠B的度数为（）

A、 $65^{\circ}$ B、 $105^{\circ}$ C、 $115^{\circ}$ D、 $125^{\circ}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} + a^{3} = 2 a^{5}$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 $a^{3} \cdot a^{5} = a^{15}$ D、 ${(a b^{2})}^{2} = a^{2} b^{4}$

查看试题解析
4. 下列各式中，不能够用平方差公式计算的是（　　）

A、(y+2x)(2x﹣y) B、(﹣x﹣3y)(x+3y) C、(2x²﹣y² )(2x²+y² ) D、(4a+b﹣c)(4a﹣b﹣c)

查看试题解析
5. 若 $a - b = 1 ， a^{2} + b^{2} = 13$ ，则 $a b$ 等于（）

A、6 B、7 C、-6 D、-7

查看试题解析
6. 《九章算术》中记载：“今有人共买物，人出八，盈三；人出七，不足四.问人数，物价各几何？”意思是：现有一些人共同买一个物品，每人出8元，还余3元；每人出7元，还差4元.问共有多少人？这个物品价格是多少元？设共有 $x$ 个人，这个物品价格是 $y$ 元.则可列方程组为（）

A、 ${\begin{array}{l} 8 x = y + 3, \\ 7 x = y - 4 \end{array}$ B、 ${\begin{array}{l} 8 x = y - 3, \\ 7 x = y + 4 \end{array}$ C、 ${\begin{array}{l} 8 x = y + 4, \\ 7 x = y - 3 \end{array}$ D、 ${\begin{array}{l} 8 x = y - 4, \\ 7 x = y + 3 \end{array}$

查看试题解析
7. 下列各式从左到右因式分解正确的是（）

A、 $2 x - 6 y + 2 = 2 (x - 3 y)$ B、 $x^{2} - 2 x + 1 = x (x - 2) + 1$ C、 $x^{2} - 4 = {(x - 2)}^{2}$ D、 $x^{3} - x = x (x + 1) (x - 1)$

查看试题解析
8. 如图，有以下四个条件：① $∠ B + ∠ B C D = 180 °$ ，② $∠ 3 = ∠ 4$ ，③ $∠ 1 = ∠ 2$ ， ④ $∠ B = ∠ 5$ ，其中不能判定 $A B / / C D$ 的是（）

A、① B、② C、③ D、④

查看试题解析
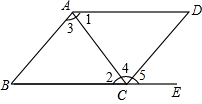9. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 2 \\ b x + a y = - 3 \end{array}$ 的解，则 $a + b$ 的值是（）

A、﹣1 B、1 C、﹣5 D、5

查看试题解析
10. 疫情无情人有情，爱心捐款传真情，新型冠状病毒感染的肺炎疫情期间，某班学生积极参加献爱心活动，该班50名学生的捐款统计情况如表：

金额/元

5

10

20

50

100

人数

6

17

14

8

5

则他们捐款金额的平均数、中位数、众数分别是（）

A、27.6，10，20 B、27.6，20，10 C、37，10，10 D、37，20，10

查看试题解析

二、填空题

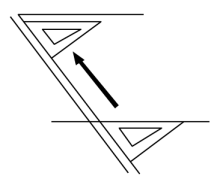
11. 如图，给出了直线外一点作已知直线平行线的一种方法，它的依据是。

查看试题解析
12. 方程组 ${\begin{matrix} x + y = 5 \\ x - 3 y = 17 \end{matrix}$ 的解是.

查看试题解析
13. 因式分解： $2 x^{2} - 18$ =

查看试题解析
14. 如图，将一块三角板的直角顶点放在直尺的一边上，当 $∠ 2 = 37 °$ 时， $∠ 1 =$ .

查看试题解析
15. 若 $a^{m} = 3$ ， $a^{n} = 5$ ，则 $a^{2 m + n}$ 的值为.

查看试题解析
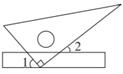16. 利用乘法公式计算： $98^{2} =$ .

查看试题解析
17. 如图所示，△COD是△AOB绕点O顺时针方向旋转35°后所得的图形，点C恰好在AB上，∠AOD＝90°，则∠BOC的度数是.

查看试题解析
18. 如图，把一张长方形纸条ABCD沿EF折叠，若∠BGD'为x度，则∠1的度数应为度(用含x的代数式表示)。

查看试题解析

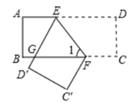
三、解答题

19.

(1)、解方程组： ${\begin{matrix} 2 x - y = 1 \\ 3 x + 2 y = 12 \end{matrix}$

(2)、计算： $(x + 1) (2 x - 3)$

查看试题解析
20. 把下列多项式因式分解：

(1)、 $x (y - 3) - (2 y - 6)$

(2)、 $- 4 a x^{2} + 12 a x - 9 a$

查看试题解析
21. 先化简，再求值： ${(x - 2 y)}^{2} + (x - 2 y) (x + 2 y)$ ，其中 $x = - 2$ ， $y = 1$ .

查看试题解析
22. 如图在边长为1的小正方形组成的网格中，△OAB的顶点都在格点上.

（ 1 ）请作出△OAB关于直线CD对称的△O₁A₁B₁；

（ 2 ）请将△OAB绕点B顺时针旋转90°，画出旋转后的△BO₂A₂.

查看试题解析
23. 如图，直线 $a ∥ b$ ， $A B$ 与 $a$ ， $b$ 分别相交于点 $A$ ， $B$ ，且 $A C ⊥ A B$ ， $A C$ 交直线 $b$ 于点 $C$ .

(1)、若 $∠ 1 = 60^{\circ}$ ，求 $∠ 2$ 的度数；

(2)、若 $A C = 5$ ， $A B = 12$ ， $B C = 13$ ，求直线 $a$ 与 $b$ 的距离.

查看试题解析
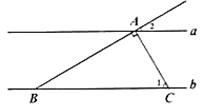24. 从A地到B地全程290千米，前一路段为国道，其余路段为高速公路．已知汽车在国道上行驶的速度为60km/h，在高速公路上行驶的速度为100km/h，一辆客车从A地开往B地一共行驶了3.5h．求A、B两地间国道和高速公路各多少千米？

查看试题解析

25. 我市某中学举行“校园好声音”歌手大赛，高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩（满分100）如图所示：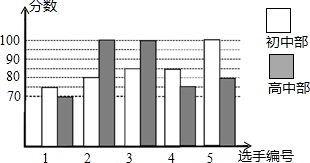

根据图示信息，整理分析数据如下表：

	平均数（分）	中位数（分）	众数（分）
初中部	$a$	85	$c$
高中部	85	$b$	100

(1)、求出表格中

a =

；

b =

；

c =

(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)、小明同学已经算出高中代表队决赛成绩的方差是：

s_{高 中}^{2} = \frac{1}{5} [{(70 - 85)}^{2} + {(100 - 85)}^{2} + {(100 - 85)}^{2} + {(75 - 85)}^{2} + {(80 - 85)}^{2}] = 160

请你计算出初中代表队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定.

查看试题解析

26. 如图1， $A B ∥ C D$ ， $∠ P A B = 130 °$ ， $∠ P C D = 120 °$ ，求 $∠ A P C$ 的度数.

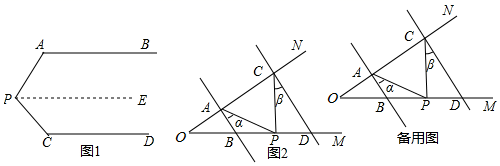
小明的思路是：过 $P$ 作 $P E / / A B$ ，通过平行线性质来求 $∠ A P C$ .

(1)、按小明的思路，求 $∠ A P C$ 的度数；

(2)、（问题迁移）：如图2， $A B / / C D$ ，点 $P$ 在射线 $O M$ 上运动，记 $∠ P A B = α$ ， $∠ P C D = β$ ，当点 $P$ 在 $B$ 、 $D$ 两点之间运动时，问 $∠ A P C$ 与 $α$ 、 $β$ 之间有何数量关系？请说明理由；

(3)、（问题应用）：在（2）的条件下，如果点 $P$ 在 $B$ 、 $D$ 两点外侧运动时（点 $P$ 与点 $O$ 、 $B$ 、 $D$ 三点不重合），请直接写出 $∠ A P C$ 与 $α$ 、 $β$ 之间的数量关系.

查看试题解析

金额/元	5	10	20	50	100
人数	6	17	14	8	5