初中数学浙教版七年级上册第二章有理数的运算单元测试

试卷更新日期：2021-08-04 类型：单元试卷

进入出卷网下载

1. 计算 $- 2 + 8$ 的结果是（）

A、－6 B、6 C、－10 D、10

查看试题解析
2. 计算﹣1▢1＝0，则“▢”表示的运算符号是（）

A、+ B、﹣ C、× D、÷

查看试题解析
3. 某地区2021年元旦的最高气温为 $9 ℃$ ，最低气温为 $- 2 ℃$ ，那么该地区这天的最低气温比最高气温低（）

A、 $7 ℃$ B、 $- 7 ℃$ C、 $11 ℃$ D、 $- 11 ℃$

查看试题解析
4. -4的倒数是（）.

A、 $- \frac{1}{4}$ B、 $\frac{1}{4}$ C、-4 D、4

查看试题解析
5. 计算 $(- 21) \div 7$ 的结果是（）

A、-3 B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
6. 据报道：今年“五一”期间，苏通大桥、崇启大桥、沪苏通大桥三座跨江大桥车流量约1370000辆次.将1370000用科学记数法表示为（）

A、 $0.137 \times 10^{7}$ B、 $1.37 \times 10^{7}$ C、 $0.137 \times 10^{6}$ D、 $1.37 \times 10^{6}$

查看试题解析

7. 生活中常用的十进制是用0~9这十个数字来表示数，满十进一，例：

12 = 1 \times 10 + 2

，

212 = 2 \times 10 \times 10 + 1 \times 10 + 2

；计算机也常用十六进制来表示字符代码，它是用0~

F

来表示0~15，满十六进一，它与十进制对应的数如下表：

十进制	0	1	2	…	8	9	10	11	12	13	14	15	16	17	…
十六进制	0	1	2	…	8	9	$A$	$B$	$C$	$D$	$E$	$F$	10	11	…

例：十六进制 $2 B$ 对应十进制的数为 $2 \times 16 + 11 = 43$ ， $10 C$ 对应十进制的数为 $1 \times 16 \times 16 + 0 \times 16 + 12 = 268$ ，那么十六进制中 $14 E$ 对应十进制的数为（）

A、28 B、62 C、238 D、334

8. 某玩具商店周年店庆，全场八折促销，持会员卡可在促销活动的基础上再打六折．某电动汽车原价300元，小明持会员卡购买这个电动汽车需要花（）元

A、240 B、180 C、160 D、144

查看试题解析
9. 用四舍五入法，865600精确到千位的近似值是（）

A、 $8.65 \times 10^{5}$ B、 $8.66 \times 10^{5}$ C、 $8.656 \times 10^{5}$ D、865000

查看试题解析
10. 某市参加中考的学生人数约为 $6.01 \times 10^{4}$ 人，对于这个近似数，下列说法正确的是 $($ $)$

A、精确到百分位 B、精确到十分位 C、精确到个位 D、精确到百位

查看试题解析

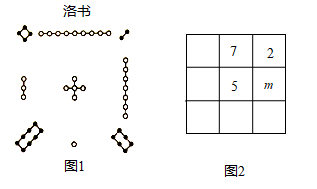
11. 计算一个式子计算器上显示的结果是 $1.597583$ ，将这个结果精确到0.01是．

查看试题解析
12. 计算： ${(- \frac{1}{2})}^{2} =$ .

查看试题解析
13. 计算： $\frac{3}{5} \div （ - 1 \frac{4}{5}) =$

查看试题解析
14. 计算： $2 \div \frac{1}{3} \times 3 =$ ．

查看试题解析
15. 用正负数表示气温的变化量，上升为正，下降为负.登山队攀登一座山峰，每登高 $1 km$ 气温的变化量为 $- 6 ° C$ ，攀登 $2 km$ 后，气温下降 $° C$ .

查看试题解析
16. 把1～9这9个数填入 $3 \times 3$ 的方格中，使其任意一行，任意一列及两条对角线上的数之和都等于15，这样便构成了一个“九宫格”，它源于我国古代的“洛书”（图1），是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”，则其中m的值为.

查看试题解析

17. 写出下列各数的倒数．
$- 2$ ， $\frac{1}{3}$ ， $- 1 \frac{1}{2}$ ， $\frac{5}{4}$ ．

查看试题解析
18. 小明和小红在做运算游戏，两人抽取的数据如图，游戏规定：长方形表示对应的数前是正号，圆形表示对应的数前是负号，计算其和，结果小者为胜，请分别计算出小明与小红最后和的结果，并说明谁获得了胜利.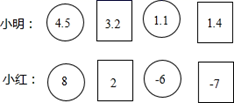

查看试题解析
19. 计算6÷（﹣ $\frac{1}{2} + \frac{1}{3}$ ），方方同学的计算过程如下，原式=6 $\div (- \frac{1}{2})$ +6 $\div \frac{1}{3}$ =﹣12+18=6．请你判断方方的计算过程是否正确，若不正确，请你写出正确的计算过程．

查看试题解析
20. 若xⁿ＝3，yⁿ＝4，求（2xⁿ）²⋅2yⁿ的值．

查看试题解析
21. 在“ $-$ ”、“ $\div$ ”两个符号中选一个自己喜欢的符号，填入 $5 \div \frac{5}{4} - 3^{2} + 2 \times (1 □ \frac{1}{2})$ 中的“ $□$ ”．并计算．

查看试题解析
22. 小丽与小明在讨论问题：
小丽：如果你把7498近似到4位数，你就会得到7000．
小明：不，我有另外一种解答方法，可以得到不同的答案，首先，将7498近似到百位，得到7500，接着再把7500近似到千位，就得到8000．
你怎样评价小丽和小明的说法呢？

查看试题解析

初中数学浙教版七年级上册第二章 有理数的运算 单元测试