湖南省邵阳二高2022届高三上学期数学7月第一次自主调研试卷

试卷更新日期：2021-08-04 类型：高考模拟

进入出卷网下载

一、单项选择题：本题共8道小题，每小题5分，共40分。

1. 已知复数 $z = \frac{3 - i}{1 + 2 i}$ （ $i$ 为虚数单位），则 $| z | =$ （）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
2. 若非零向量 $\vec{a}$ 、 $\vec{b}$ 满足 $| \vec{a} | = 2 | \vec{b} | = 4 ， (\vec{a} - 2 \vec{b}) \cdot \vec{a} = 0$ ，则 $\vec{a}$ 、 $\vec{b}$ 两向量的夹角为（）

A、0° B、60° C、90° D、180°

查看试题解析
3. 已知集合 $A= {x | - 1 \leq 2 x + 1 \leq 3} ， B = {x | | x - \frac{1}{2} | + | x - \frac{3}{2} | < 2}$ ，则 $A \cap B =$ （）

A、 ${x | - 1 \leq x < 0}$ B、 ${x | 0 < x \leq 1}$ C、 ${x | 0 \leq x \leq 2}$ D、 ${x | 0 \leq x \leq 1}$

查看试题解析
4. 从包含甲在内的5名学生中选出4名分别参加数学、物理、化学、生物学科竞赛，其中甲不能参加生物竞赛，则不同的参赛方案种数为（）

A、48 B、72 C、90 D、96

查看试题解析
5. 已知 $\cos^{2} (\frac{x}{2} + \frac{π}{4}) = \cos (x + \frac{π}{6})$ ，则cosx等于（）

A、 $\frac{1}{3}$ B、 $- \frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $- \frac{1}{3}$

查看试题解析
6. 若 $a > b > 1$ ， $0 < c < 1$ ，则下列式子成立的是（）

A、 $\log_{a} c < \log_{b} c$ B、 $\frac{b}{a - c} > \frac{a}{b - c}$ C、 $b \log_{a} c > a \log_{b} c$ D、 $a^{b} < b^{a}$

查看试题解析
7. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，过 $F_{2}$ 且斜率为 $- 1$ 的直线与其左支交于点 $P$ ，若存在 $λ (0 < λ < 1)$ ，使 $\vec{F_{2} Q} = λ \vec{F_{2} P}$ ， $\vec{F_{1} Q} \cdot \vec{F_{2} P} = 0$ ，且 $\frac{\vec{F_{2} F_{1}} \cdot \vec{F_{2} P}}{| \vec{F_{2} P} |} \cdot \frac{\vec{P F_{1}} \cdot \vec{P F_{2}}}{| P F_{2} |} = {| \vec{F_{1} Q} |}^{2}$ ，则双曲线的离心率为（）

A、 $\sqrt{3} + 1$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{2} + 1$

查看试题解析
8. 设 $k > 0$ ，若存在正实数 $x$ ，使得不等式 $\log_{27} x - k \cdot 3^{k x - 1} \geq 0$ 成立，则 $k$ 的最大值为（）

A、 $\frac{1}{e \ln 3}$ B、 $\frac{\ln 3}{e}$ C、 $\frac{e}{\ln 3}$ D、 $\frac{\ln 3}{2}$

查看试题解析

二、多项选择题：本题共4小题，每小题5分，共20分。

9. 下列说法正确的是（）

A、命题“ $\exists x_{0} \in R$ ， $x_{0}^{2} + 2 x_{0} + m \leq 0$ ”的否定是“ $\forall x \in R$ ， $x^{2} + 2 x + m > 0$ ” B、已知 $a \in R$ ，则“ $a \leq 1$ ”是“ $a^{2} \leq a$ ”的必要不充分条件 C、命题 $p$ ：若 $α$ 为第一象限角，则 $\sin α < α$ ；命题 $q$ ：函数 $f (x) = 2^{x} - x^{2}$ 有两个零点，则 $\neg p \lor \neg q$ 为假命题 D、 $\exists x_{0} \in (0 ， \frac{1}{3})$ ， ${(\frac{1}{2})}^{x_{0}} > \log_{\frac{1}{3}} x_{0}$

查看试题解析
10. 设函数 $f (x) = a \sin 2 x + b \cos 2 x (a ， b \in R)$ ，则下列说法正确的有（）

A、当 $a = 1$ ， $b = 0$ 时， $f (x)$ 为奇函数 B、当 $a = 1$ ， $b = - 1$ 时， $f (x)$ 的一个对称中心为 $(\frac{3 π}{8} ， 0)$ C、若关于 $x$ 的方程 $a \sin 2 x + b \cos 2 x = m$ 的正实根从小到大依次构成一个等差数列，则这个等差数列的公差为 $π$ D、当 $a = 1$ ， $b = - \sqrt{3}$ 时， $f (| \frac{x}{2} |)$ 在区间 $(- 2 π ， 2 π)$ 上恰有4个零点

查看试题解析
11. 已知抛物线C：x²=4y的焦点为F，A、B在抛物线C上，且 $\vec{A F}$ =2 $\vec{F B}$ ，过A，B分别引抛物线C两切线交于点P，则下列结论正确的是（）

A、点P位于抛物线的准线上 B、∠APB=90° C、PF⊥AB D、PF=2 $\sqrt{2}$

查看试题解析
12. 如图，菱形 $A B C D$ 边长为 $2$ ， $∠ B A D = 60 °$ ， $E$ 为边 $A B$ 的中点．将 $△ A D E$ 沿 $D E$ 折起，使 $A$ 到 $A^{'}$ ，且平面 $A^{'} D E ⊥$ 平面 $B C D E$ ，连接 $A^{'} B$ ， $A^{'} C$ ．

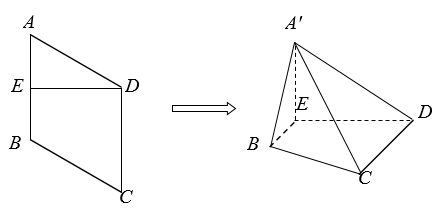
则下列结论中正确的是（）

A、 $B D ⊥ A^{'} C$ B、四面体 $A^{'} C D E$ 的外接球表面积为 $8 π$ C、 $B C$ 与 $A^{'} D$ 所成角的余弦值为 $\frac{3}{4}$ D、直线 $A^{'} B$ 与平面 $A^{'} C D$ 所成角的正弦值为 $\frac{\sqrt{6}}{4}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分。

13. 曲线 $y = \cos x - \frac{x}{2}$ 在点 $(0, 1)$ 处的切线方程为.

查看试题解析
14. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n} (n \in N^{*})$ ，公差 $d \neq 0$ ， $S_{6} = 90$ ， $a_{7}$ 是 $a_{3}$ 与 $a_{9}$ 的等比中项，则 ${a_{n}}$ 的通项公式为.

查看试题解析
15. 中国工程院院士袁隆平，被誉为“世界杂交水稻之父”．他发明的“三系法”籼型杂交水稻，创建了超级杂交稻技术体系．某地种植超级杂交稻，产量从第一期大面积亩产 $760$ 公斤，到第二期亩产 $810$ 公斤，第三期亩产 $860$ 公斤，第四期亩产 $1030$ 公斤．将第一期视为第二期的父代，第二期视为第三期的父代，或第一期视为第三期的祖父代，并且认为子代的产量与父代的产量有关，请用线性回归分析的方法预测第五期的产量为每亩公斤．
附：用最小二乘法求得线性回归方程为 $\hat{y} = \hat{b} x + \hat{a}$ ，其中 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

查看试题解析
16. 英国数学家泰勒发现了公式： $\sin x = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + \dots$ ，瑞士大数学家欧拉凭着他非凡的数学洞察力，由此公式得到了下面的无穷级数之和，并最终给出了严格证明．
$1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + \dots$ ．其发现过程简单分析如下：

当 $x \neq 0$ 时，有 $\frac{\sin x}{x} = 1 - \frac{x^{2}}{3!} + \frac{x^{4}}{5!} - \frac{x^{6}}{7!} + \dots$ ，

容易看出方程 $\frac{\sin x}{x} = 0$ 的所有解为： $\pm π$ ， $\pm 2 π$ ， $\dots$ ， $\pm n π$ ， $\dots$ ，

于是方程 $\frac{\sin x}{x} = 0$ 可写成： $(x^{2} - π^{2}) [x^{2} - {(2 π)}^{2}] \dots [x^{2} - {(n π)}^{2}] \dots = 0$ ，

改写成： $(1 - \frac{x^{2}}{π^{2}}) [1 - \frac{x^{2}}{2^{2} π^{2}}] \dots [1 - \frac{x^{2}}{n^{2} π^{2}}] \dots = 0$ ．（*）

比较方程（*）与方程 $1 - \frac{x^{2}}{3!} + \frac{x^{4}}{5!} - \frac{x^{6}}{7!} + \dots = 0$ 中 $x^{2}$ 项的系数，即可得

$1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + \dots =$ ．

查看试题解析

四、解答题：本题共6小题，共70分。

17. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ， $2 \sin A \cos B = 2 \sin C + \sin B$ .

(1)、求角A；

(2)、若 $a = 4$ ， $b + c = 2 \sqrt{5}$ ，求 $△ A B C$ 的面积.

查看试题解析
18. 已知数列 ${\log_{k} a_{n}}$ 是首项为4，公差为2的等差数列.( $k$ 为常数， $k > 0$ 且 $k \neq 1$ ).
(Ⅰ)求证：数列 ${a_{n}}$ 是等比数列；

(Ⅱ)当 $k = \sqrt{2}$ 时，设 $a_{n} b_{n} = \frac{2^{n + 1}}{4 n^{2} - 1}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
19. 如图，在五面体 $A B C D E F$ 中，面 $A D E F$ 为矩形，且与面 $A B C D$ 垂直， $∠ B C D = 90 °$ ， $A D = C D = \frac{1}{2} B C = 1$ ， $D E = \sqrt{2}$ .

(1)、证明： $A D // B C$ ；

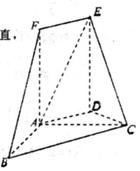(2)、求平面 $A C E$ 与平面 $B C E F$ 所成的锐二面角的余弦值.

查看试题解析

20. 从某企业生产的某种产品中抽取1000件，测量这些产品的一项质量指标值，由测量结果得如下频率分布表和频率分布直方图．

分组	频数	频率
[2.5，7.5)	2	0.002
[7.5，12.5)	m	0.054
[12.5，17.5)	106	0.106
[17.5，22.5)	149	0.149
[22.5，27.5)	352	n
[27.5，32.5)	190	0.190
[32.5，37.5)	100	0.100
[37.5，42.5)	47	0.047
合计	1000	1.000

附： $\sqrt{52.6} \approx 7.25$ ， $P (μ - σ < x < μ + σ) = 0.6826$ ， $P (μ - 2 σ < x < μ + 2 σ) = 0.9544$ ．

(1)、求m，n，a的值；

(2)、求出这1000件产品质量指标值的样本平均数

\bar{x}

（同一组中的数据用该组区间的中点值作代表）；

(3)、

\bar{x} = 5 \times 0.002 + 10 \times 0.054 + 15 \times 0.106 + 20 \times 0.149 + 25 \times 0.352 + 30 \times 0.190 + 35 \times 0.1 + 40 \times 0.047 = 25

由直方图可以认为，这种产品的质量指标值

Z

服从正态分布

N (μ ， σ^{2})

，其中

μ

近似为样本平均数

\bar{x}

，

σ^{2}

近似为样本方差

s^{2}

，其中已计算得

σ^{2} = 52.6

．如果产品的质量指标值位于区间

(10.50 ， 39.50)

，企业每件产品可以获利10元，如果产品的质量指标值位于区间

(10.50 ， 39.50)

之外，企业每件产品要损失100元，从该企业一天生产的产品中随机抽取20件产品，记

X

为抽取的20件产品所获得的总利润，求

E X

．

查看试题解析

21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 （ a > b > 0 ）$ 的长轴长为 $4$ ，离心率为 $\frac{\sqrt{3}}{2}$ ，

(1)、求椭圆 $C$ 的方程；

(2)、过椭圆 $C$ 上的点 $A (x_{0} ， y_{0})$ $（ x_{0} y_{0} \neq 0 ）$ 的直线 $l$ 与 $x$ ， $y$ 轴的交点分别为 $M$ ， $N$ ，且 $\vec{A N} = 2 \vec{M A}$ ，过原点 $O$ 的直线 $m$ 与 $l$ 平行，且与 $C$ 交于 $B$ ， $D$ 两点，求 $△ A B D$ 面积的最大值．

查看试题解析
22. 已知函数 $f (x) = e^{x} (2 x - \frac{1}{2} x^{2}) - a (x - 1)$ ， $a \in R$ ， $e = 2 .718 28 \dots$ 是自然对数的底数．

(1)、当 $a = 0$ 时，讨论 $f (x)$ 的单调性；

(2)、当 $x \leq 2$ 时， $f (x) \geq 0$ ，求 $a$ 的取值范围．

查看试题解析