安徽省滁州市定远县重点中学2020-2021学年高二上学期理数10月月考试卷
试卷更新日期:2021-08-04 类型:月考试卷
一、单选题
-
1. 已知两点 , ,直线l过点 且与线段AB相交,则直线的斜率k的取值范围是( )A、 B、 或 C、 D、2. 已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
137
966
191
925
271
932
812
458
569
683
431
257
393
027
556
488
730
113
537
989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A、0.40 B、0.30 C、0.35 D、0.253. 据全球权威票房网站Mojo数据统计,截至8月20日14时,《战狼2》国内累计票房50亿,截至目前,《战狼2》中国市场观影人次达1.4亿,这一数字也创造了全球影史“单一市场观影人次”的新记录,为了解《战狼2》观影人的年龄分布情况,某调查小组随机统计了100个此片的观影人的年龄(他们的年龄都在区间 内),并绘制了如图所示的频率分布直方图,则由图可知,这100人年龄的中位数为( ) A、33 B、34 C、35 D、364. 某几何体的三视图如图所示,且该几何体的体积是3,则正视图中 的值是( )
A、33 B、34 C、35 D、364. 某几何体的三视图如图所示,且该几何体的体积是3,则正视图中 的值是( ) A、2 B、 C、 D、35. 已知点 是直线 上一动点, , 是圆 的两条切线, , 是切点.若四边形 的最小面积是2,则 的值为( )A、 B、 C、 D、26. 阅读如图所示的程序框图,运行相应的程序,则输出 的值为( )
A、2 B、 C、 D、35. 已知点 是直线 上一动点, , 是圆 的两条切线, , 是切点.若四边形 的最小面积是2,则 的值为( )A、 B、 C、 D、26. 阅读如图所示的程序框图,运行相应的程序,则输出 的值为( )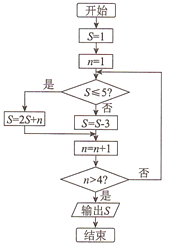 A、5 B、11 C、14 D、197. 已知直线 为圆 在点 处的切线,点 为直线 上一动点,点 为圆 上一动点,则 的最小值为( )A、 B、 C、 D、8. 设点 在直线 上,若 ,且 恒成立,则 的值( )A、2 B、4 C、6 D、89. 是两个平面, 是两条直线,有下列四个命题:
A、5 B、11 C、14 D、197. 已知直线 为圆 在点 处的切线,点 为直线 上一动点,点 为圆 上一动点,则 的最小值为( )A、 B、 C、 D、8. 设点 在直线 上,若 ,且 恒成立,则 的值( )A、2 B、4 C、6 D、89. 是两个平面, 是两条直线,有下列四个命题:①如果 ,那么 .
②如果 ,那么 .
③如果 ,那么 .
④如果 ,那么 与 所成的角和 与 所成的角相等.
其中正确的命题为( )
A、②③④ B、①②④ C、①③④ D、①②④10. 如图,在正方体 中,棱长为1, 分别为 与 的中点, 到平面 的距离为( ) A、 B、 C、 D、11. 某校高一年级有甲,乙,丙三位学生,他们前三次月考的物理成绩如表:
A、 B、 C、 D、11. 某校高一年级有甲,乙,丙三位学生,他们前三次月考的物理成绩如表:第一次月考物理成绩
第二次月考物理成绩
第三次月考物理成绩
学生甲
80
85
90
学生乙
81
83
85
学生丙
90
86
82
则下列结论正确的是( )
A、甲,乙,丙第三次月考物理成绩的平均数为86 B、在这三次月考物理成绩中,甲的成绩平均分最高 C、在这三次月考物理成绩中,乙的成绩最稳定 D、在这三次月考物理成绩中,丙的成绩方差最大12. 三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2 , 设勾股中勾股比为 ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在红(朱)色图形内的图钉数大约为( )(参考数据: ) A、866 B、500 C、300 D、134
A、866 B、500 C、300 D、134二、填空题
-
13. 如图所示, 是棱长为 的正方体, 分别是下底面的棱 的中点, 是上底面的棱 上的一点, ,过 的平面交上底面于 , 在 上,则 .
 14. 已知线段 两端点的坐标分别为 和 ,若直线 与线段 有交点,则实数 的取值范围是.15. 已知一个 进制的数 与二进制的数 相等,那么 等于 .16. 天气预报说,在今后的三天中,每一天下雨的概率均为 .现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
14. 已知线段 两端点的坐标分别为 和 ,若直线 与线段 有交点,则实数 的取值范围是.15. 已知一个 进制的数 与二进制的数 相等,那么 等于 .16. 天气预报说,在今后的三天中,每一天下雨的概率均为 .现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:488 932 812 458 989 431 257 390 024 556
734 113 537 569 683 907 966 191 925 271
据此估计,这三天中恰有两天下雨的概率近似为.
三、解答题
-
17. 已知直线 , ,圆 .(1)、证明:直线 恒过一定点 ;(2)、证明:直线 与圆 相交;(3)、当直线 被圆 截得的弦长最短时,求 的值.18. 为了解消费者购物情况,某购物中心在电脑小票中随机抽取 张进行统计,将结果分成6组,分别是: , ,制成如下所示的频率分布直方图(假设消费金额均在 元的区间内).(1)、若在消费金额为 元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票来自 元和 元区间(两区间都有)的概率;(2)、为做好春节期间的商场促销活动,商场设计了两种不同的促销方案.

方案一:全场商品打八五折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由.
19. 如图所示,该几何体是由一个直三棱柱 和一个正四棱锥 组合而成, , .
(Ⅰ)证明:平面 平面 ;
(Ⅱ)求正四棱锥 的高 ,使得二面角 的余弦值是 .
20. 2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与 的数据如表:时间
星期一
星期二
星期三
星期四
星期五
星期六
星期日
车流量 (万辆)
1
2
3
4
5
6
7
的浓度 (微克/立方米)
28
30
35
41
49
56
62
(1)、由散点图知 与 具有线性相关关系,求 关于 的线性回归方程;(提示数据: )(2)、利用(1)所求的回归方程,预测该市车流量为 12 万辆时 的浓度.参考公式:回归直线的方程是 ,
其中 .
