初中数学浙教版九年级上册第二章 简单事件的概率 单元测试
试卷更新日期：2021-08-03 类型：单元试卷
一、单选题
-
1. “14人中至少有2人在同一个月过生日”这一事件发生的概率为P，则（ ）A、P＝0 B、0＜P＜1 C、P＝1 D、P＞12. 一只不透明的袋子中装有3个黑球和2个白球，这些除颜色外无其他差别，从中任意摸出3个球，下列事件是必然事件的为（ ）A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球3. 下列事件中属于必然事件的是（ ）A、任意画一个三角形，其内角和是180° B、打开电视机，正在播放新闻联播 C、随机买一张电影票，座位号是奇数号 D、掷一枚质地均匀的硬币，正面朝上4. 不透明的袋子中有3个白球和2个紅球，这些球除颜色外无其他差別，从袋子中随机摸出1个球，恰好是白球的概率（ ）A、 B、 C、 D、5. 现有4张卡片，正面图案如图所示，它们除此之外完全相同.把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片正面图案恰好是“天问”和“九章”的概率是（ ）
A、 B、 C、 D、6. 经过某路口的汽车，可能直行，也可能左拐或右拐．假设这三种可能性相同，现有两车经过该路口，恰好有一车直行，另一车左拐的概率为（ ）A、 B、 C、 D、7. 某林业局将一种树苗移植成活的情况绘制成如下统计图，由此可估计这种树苗移植成活的概率约为（ ）
A、0.95 B、0.90 C、0.85 D、0.808. 某鱼塘里养了1600条鲤鱼，若干条草鱼和800条鲢鱼，该鱼塘主通过多次捕捞试验后发现，捕到草鱼的频率稳定在0.5附近，则该鱼塘捞到鲢鱼的概率约为（ ）A、 B、 C、 D、9. 从一盒写有“鲜肉3只、蛋黄2只、豆沙2只、排骨3只”的端午粽子（所有粽子的形状大小都一样）礼盒中，随机取出一只粽子，正好是蛋黄粽子的概率是（ ）A、 B、 C、 D、10. 随机掷一枚质地均匀的硬币两次，落地后至多有一次正面朝下的概率为（ ）A、 B、 C、 D、二、填空题
-
11. 社团课上，同学们进行了“摸球游戏”：在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球，将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程.整理数据后，制作了“摸出黑球的频率”与“摸球的总次数”的关系图象如图所示，经分析可以推断盒子里个数比较多的是（填“黑球”或“白球”）.
12. “打开我们七年级下册的数学教科书，正好翻到第60页”，这是（填“随机”或“必然”）事件.13. 动物学家通过大量的调查，估计某种动物活到20岁的概率为0.8，活到25岁的概率为0.5，据此若设刚出生的这种动物共有a只．则20年后存活的有只，现年20岁的这种动物活到25岁的概率是 ．14. 小红的口袋有3把钥匙，分别能打开甲、乙、丙三把锁，他从口袋中任意取出一把钥匙，能打开甲锁的概率是.15. 某农场引进一批新菜种，在播种前做了五次发芽实验，每次任取一定数量的种子进行实验． 实验结果如下表所示 ：实验的菜种数
200
500
1000
2000
10000
发芽的菜种数
193
487
983
1942
9734
发芽率
0.965
0.974
0.983
0.971
0.973
在与实验条件相同的情况下，估计种一粒这样的菜种发芽的概率为 ． （ 精确到 0.01 ）
16. 贵阳市2021年中考物理实验操作技能测试中，要求学生两人一组合作进行，并随机抽签决定分组.有甲、乙、丙、丁四位同学参加测试，则甲、乙两位同学分到同一组的概率是.三、解答题
-
17. 下列第一排表示各盒中球的情况，第二排的语言描述了摸到篮球的可能性大小，请你用线把第一排盒子与第二排的描述连接起来使之相符．
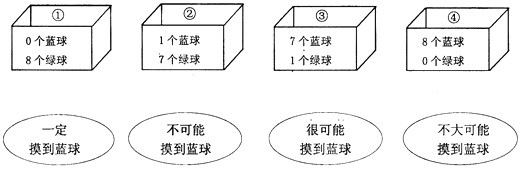18. 在一个不透明的口袋中装有三个小球，分别标记数字1、2、3，每个小球除数字不同外其余均相同，小明和小亮玩摸球游戏，两人各摸一个球，谁摸到的数字大谁获胜，摸到相同数字记为平局．小明从口袋中摸出一个小球记下数字后放回并搅匀，小亮再从口袋中摸出一个小球．用画树状图（或列表）的方法，求小明获胜的概率．19. 如图，甲、乙两个转盘均被分成3个面积相等的扇形，每个扇形中都标有相应的数字，同时转动两个转盘（当指针指在边界线上时视为无效，需重新转动转盘），当转盘停止后，把甲、乙两个转盘中指针所指数字分别记为x ， y ． 请用树状图或列表法求点 落在平面直角坐标系第一象限内的概率．
20. “2015扬州鉴真国际半程马拉松”的赛事共有三项：A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”．小明参加了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．（1）小明被分配到“迷你马拉松”项目组的概率．
（2）为估算本次赛事参加“迷你马拉松”的人数，小明对部分参赛选手作如下调查：
调查总人数
50
100
200
500
1000
参加“迷你马拉松”人数
21
45
79
200
401
参加“迷你马拉松”频率
0.360
0.450
0.395
0.400
0.401
①请估算本次赛事参加“迷你马拉松”人数的概率 ．（精确到0.1）
②若本次参赛选手大约有30000人，请你估计参加“迷你马拉松”的人数是多少？
21. 某封闭的纸箱中有红色、黄色的玻璃球若干，为了估计出纸箱中红色、黄色球的数目，小亮向纸箱中放入25个白球，通过多次摸球实验后，发现摸到白球的频率为25％，摸到黄球的频率为40％，试估计出原纸箱中红球、黄球的数目．
22. 小明和小刚一起做游戏，游戏规则如下：将分别标有数字 1， 2， 3， 4 的 4 个小球放入一个不透明的袋子中，这些球除数字外都相同．从中随机摸出一个球记下数字后放回，再从中随机摸出一个球记下数字．若两次数字差的绝对值小于 2，则小明获胜，否则小刚获胜．这个游戏对两人公平吗？请说明理由．23. 小颖和小亮都想去观看“垃圾分类”宣传演出，但只有一张入场券，于是他们设计了一个“配紫色”游戏： ， 是两个可以自由转动的转盘，每个转盘都被分成面积相等的几个扇形，同时转动两个转盘，如果其中一个转盘转出了红色，另一个转盘转出了蓝色，那么可以配成紫色.若配成紫色，则小颖去观看，否则小亮去观看.这个游戏对双方公平吗？请用画树状图或者列表的方式说明理由.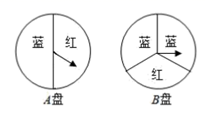
四、综合题
-
24. 圆周率 是无限不循环小数.历史上，祖冲之、刘徽、韦达、欧拉等数学家都对 有过深入的研究.目前，超级计算机已计算出 的小数部分超过31.4万亿位.有学者发现，随着 小数部分位数的增加，0~9这10个数字出现的频率趋于稳定，接近相同.
(1)、从 的小数部分随机取出一个数字，估计数字是6的概率为；(2)、某校进行校园文化建设，拟从以上4位科学家的画像中随机选用2幅，求其中有一幅是祖冲之的概率.（用画树状图或列表方法求解）