初中数学浙教版九年级上册第一章 二次函数 单元测试
试卷更新日期:2021-08-03 类型:单元试卷
一、单选题
-
1. 一个边长为2厘米的正方形,如果它的边长增加 厘米,则面积随之增加 平方厘米,那么 与 之间满足的函数关系是( )A、正比例函数 B、反比例函数 C、一次函数 D、二次函数2. 若y=(m﹣1) 是关于x的二次函数,则m的值为( )A、﹣2 B、﹣2或1 C、1 D、不存在3. 二次函数的图象如图所示, 则这个二次函数的表达式为( )
 A、 B、 C、 D、4. 将二次函数y=(x﹣3)2+k的图象向上平移5个单位,若平移后的函数图象与直线y=2没有交点,则k的取值范围是( )A、k<﹣3 B、k≤﹣3 C、k>﹣3 D、k≥﹣35. 把二次函数 的图象作关于 轴的对称变换,所得图象的解析式为 ,则a与b满足的关系是( )A、b=a B、b=2a C、a+b=0 D、2a+b=06. 若二次函数y=x2+2x+k的图象经过点(1,y1),(-2,y2),则y1与y2的大小关系为( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定7. 若点A(﹣1,y1),B(2,y2),C(3,y3)在抛物线y=﹣2x2+8x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y2<y1 B、y2<y1<y3 C、y1<y3<y2 D、y3<y1<y28. 王芳将如图所示的三条水平直线m1 , m2 , m3的其中一条记为x轴(向右为正方向),三条竖直直线m4 , m5 , m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2﹣6ax﹣2.5,则她所选择的x轴和y轴分别为( )
A、 B、 C、 D、4. 将二次函数y=(x﹣3)2+k的图象向上平移5个单位,若平移后的函数图象与直线y=2没有交点,则k的取值范围是( )A、k<﹣3 B、k≤﹣3 C、k>﹣3 D、k≥﹣35. 把二次函数 的图象作关于 轴的对称变换,所得图象的解析式为 ,则a与b满足的关系是( )A、b=a B、b=2a C、a+b=0 D、2a+b=06. 若二次函数y=x2+2x+k的图象经过点(1,y1),(-2,y2),则y1与y2的大小关系为( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定7. 若点A(﹣1,y1),B(2,y2),C(3,y3)在抛物线y=﹣2x2+8x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y2<y1 B、y2<y1<y3 C、y1<y3<y2 D、y3<y1<y28. 王芳将如图所示的三条水平直线m1 , m2 , m3的其中一条记为x轴(向右为正方向),三条竖直直线m4 , m5 , m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2﹣6ax﹣2.5,则她所选择的x轴和y轴分别为( ) A、m1 , m4 B、m2 , m3 C、m3 , m6 D、m4 , m59. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )
A、m1 , m4 B、m2 , m3 C、m3 , m6 D、m4 , m59. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )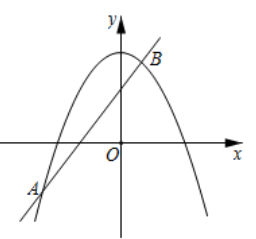 A、 或 B、 或 C、 D、10. 将二次函数 的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线 与新函数的图象恰有3个公共点时,b的值为( )
A、 或 B、 或 C、 D、10. 将二次函数 的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线 与新函数的图象恰有3个公共点时,b的值为( )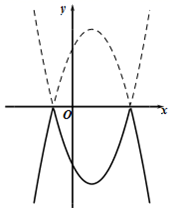 A、 或 B、 或 C、 或 D、 或
A、 或 B、 或 C、 或 D、 或二、填空题
-
11. 抛物线 的对称轴为直线 .12. 在平面直角坐标系 中,若抛物线 与x轴只有一个交点,则 .13. 若二次函数y=﹣x2+6x﹣m的图象与x轴没有交点,则m的取值范围是 .14. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,抛物线 的顶点P在线段 上,与x轴相交于C、D两点,设点C、D的横坐标分别为 、 ,且 .若 的最小值是 ,则 的最大值是 .
 15. 已知点 P (x1 , y1 ), Q (x2 , y2)都在抛物线 y = x2-4x + 4上,若 x1 + x2 = 4,则y1 y2 .(填“>"、“<"或“=”)16. 抛物线 向右平移1个单位,再向下平移2个单位,平移后的抛物线的顶点坐标是 .
15. 已知点 P (x1 , y1 ), Q (x2 , y2)都在抛物线 y = x2-4x + 4上,若 x1 + x2 = 4,则y1 y2 .(填“>"、“<"或“=”)16. 抛物线 向右平移1个单位,再向下平移2个单位,平移后的抛物线的顶点坐标是 .三、解答题
-
17. 用配方法把二次函数y=﹣2x2+6x+4化为y=a(x+m)2+k的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.18. 已知抛物线的顶点是(-2,3),且经过点(-1,4),求这条抛物线的函数表达式.19. 已知实数a , b满足a﹣b=1,a2﹣ab+1>0,当2≤x≤3时,二次函数y=a(x﹣1)2+1(a≠0)的最大值是3,求a的值.20. 某超市购进一种商品,进货单价为每件10元在销售过程中超市按相关规定.销售单价不低于1元且不高于19元如果该商品的销售单价x(单位:元/件)与日销售量y(单位:件)满足一次函数关系 ,设该商品的日销售利润为w元,那么当该商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?21. 如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),求当矩形ABCD的面积最大时AB的长.
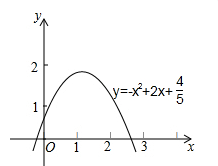
 22. 根据设计图纸已知:所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+ ,求喷出的水流距水平面的最大高度是多少?
22. 根据设计图纸已知:所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+ ,求喷出的水流距水平面的最大高度是多少?
四、综合题
-
23. 已知抛物线 经过点 和 .(1)、求 、 的值;(2)、将该抛物线向上平移2个单位长度,再向右平移1个单位长度,得到新的抛物线,直接写出新的抛物线相应的函数表达式.24. 某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅列出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应值数据.
x
40
70
90
y
180
90
30
W
3600
4500
2100
(1)、求y关于x的函数解析式(不要求写出自变量的取值范围);(2)、若该商品进价a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;(3)、因疫情期间,该商品进价提高了m(元/件)( ),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.