初中数学华师大版九年级上学期第23章 23.3 相似三角形 同步练习
试卷更新日期:2021-08-03 类型:同步测试
一、单选题
-
1. 如图所示,在10倍的放大镜下看到的三角形与原三角形相比,下面各个备选答案的量中,保持不变的量是( )
 A、角 B、边长 C、周长 D、面积2. 两个相似三角形的相似比是1:4,那么它们的面积比是( )A、1:2 B、1:4 C、1:16 D、1:3. 如图,在 中, , , 的周长是 ,则 的周长是( )
A、角 B、边长 C、周长 D、面积2. 两个相似三角形的相似比是1:4,那么它们的面积比是( )A、1:2 B、1:4 C、1:16 D、1:3. 如图,在 中, , , 的周长是 ,则 的周长是( ) A、 B、 C、 D、4. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )
A、 B、 C、 D、4. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )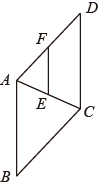 A、11 B、22 C、33 D、445. 如图,在 中, , 于点 , , , ,则 的长是( )
A、11 B、22 C、33 D、445. 如图,在 中, , 于点 , , , ,则 的长是( )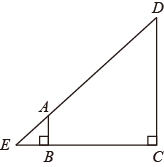 A、14 B、12.4 C、10.5 D、9.36. 如图,在平行四边形 中,点E是边 上一点,且 , 交对角线 于点F,则 等于( )
A、14 B、12.4 C、10.5 D、9.36. 如图,在平行四边形 中,点E是边 上一点,且 , 交对角线 于点F,则 等于( )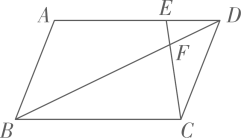 A、 B、 C、 D、7. 如图, ,下列说法错误的是( )
A、 B、 C、 D、7. 如图, ,下列说法错误的是( ) A、两个三角形是位似图形 B、点A是两个三角形的位似中心 C、点B与点 D、点C与点E是对应位似点 D. 是相似比8. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、9. 《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形 ,东边城墙 长9里,南边城墙 长7里,东门点 ,南门点 分别位于 , 的中点, , , 里, 经过 点,则 的长为( )
A、两个三角形是位似图形 B、点A是两个三角形的位似中心 C、点B与点 D、点C与点E是对应位似点 D. 是相似比8. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、9. 《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形 ,东边城墙 长9里,南边城墙 长7里,东门点 ,南门点 分别位于 , 的中点, , , 里, 经过 点,则 的长为( )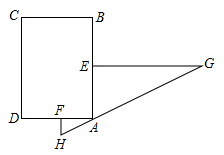 A、0.95里 B、1.05里 C、2.05里 D、2.15里10. 如图,已知 , , ,点E为射线 上一个动点,连接 ,将 沿 折叠,点B落在点 处,过点 作 的垂线,分别交 , 于M , N两点,当 为线段 的三等分点时, 的长为( )
A、0.95里 B、1.05里 C、2.05里 D、2.15里10. 如图,已知 , , ,点E为射线 上一个动点,连接 ,将 沿 折叠,点B落在点 处,过点 作 的垂线,分别交 , 于M , N两点,当 为线段 的三等分点时, 的长为( )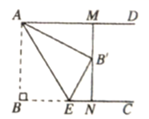 A、 B、 C、 或 D、 或
A、 B、 C、 或 D、 或二、填空题
-
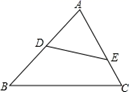
11. 已知 ,它们的周长分别为 和 ,则 与 面积之比为.12. 如图,当∠AED=时,△ADE与△ABC相似.
 13. 下列命题中,正确命题的个数为.
13. 下列命题中,正确命题的个数为.①所有的正方形都相似
②所有的菱形都相似
③边长相等的两个菱形都相似
④对角线相等的两个矩形都相似
14. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.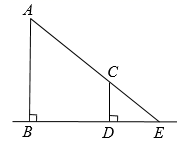 15. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=.
15. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=. 16. 如图,在△ABC中,AB=BC=2 ,AE⊥BC , 垂足为点E , 延长AE至点D , 使AD=AB , 连接CD、BD , 若∠ACD=90°,则BD的长为 .
16. 如图,在△ABC中,AB=BC=2 ,AE⊥BC , 垂足为点E , 延长AE至点D , 使AD=AB , 连接CD、BD , 若∠ACD=90°,则BD的长为 . 17. 如图,在矩形 中, , 为边 上两点,将矩形 沿 折叠,点 恰好落在 上的 处,且 ,再将矩形 沿过点 的直线折叠,使点 落在 上的 处,折痕交 于点 ,将矩形 再沿 折叠, 与 恰好重合,已知 ,则 .
17. 如图,在矩形 中, , 为边 上两点,将矩形 沿 折叠,点 恰好落在 上的 处,且 ,再将矩形 沿过点 的直线折叠,使点 落在 上的 处,折痕交 于点 ,将矩形 再沿 折叠, 与 恰好重合,已知 ,则 .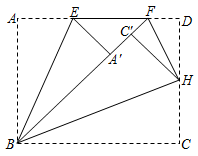
三、解答题
-
18. 如图,已知 ,求证: .
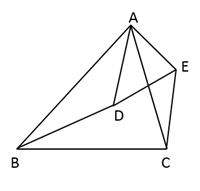 19. 青龙寺是西安最著名的櫻花观赏地,品种达到了13种之多,每年3、4月陆续开放的櫻花让这里成为了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(櫻花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆 ,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离 米.已知 米, 米, 米,点C、F、H、A在一条直线上,点M在 上, , , , .根据以上测量过程及测量数据,请你求出这棵樱花树 的高度.
19. 青龙寺是西安最著名的櫻花观赏地,品种达到了13种之多,每年3、4月陆续开放的櫻花让这里成为了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(櫻花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆 ,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离 米.已知 米, 米, 米,点C、F、H、A在一条直线上,点M在 上, , , , .根据以上测量过程及测量数据,请你求出这棵樱花树 的高度.
四、作图题
-
20. 如图,△ABC是正方形网格图中的格点三角形(顶点在格点上),请分别在图1和图2的正方形网格内按下列要求画出格点三角形.
 (1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .
(1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .五、综合题