初中数学华师大版九年级上学期第23章 23.3.3 相似三角形的性质 同步练习
试卷更新日期:2021-08-03 类型:同步测试
一、单选题
-
1. 若相似三角形的相似比为1:4,则面积比为( )A、1:16 B、16:1 C、1:4 D、1:22. 如图,已知 ∽ ,则下列哪条线段与 的比等于相似比( ).
 A、 B、 C、 D、3. 如图,赵师傅透过平举的放大镜从正上方看水平桌面上的菱形图案的一角,那么∠A与放大镜中的∠C的大小关系是( )
A、 B、 C、 D、3. 如图,赵师傅透过平举的放大镜从正上方看水平桌面上的菱形图案的一角,那么∠A与放大镜中的∠C的大小关系是( ) A、∠A=∠C B、∠A>∠C C、∠A<∠C D、无法比较4. 如图,在△ABC中,点D , 点E分别在边AB , AC上(不与端点重合),连接DE , 若DE∥BC , 则 =( )
A、∠A=∠C B、∠A>∠C C、∠A<∠C D、无法比较4. 如图,在△ABC中,点D , 点E分别在边AB , AC上(不与端点重合),连接DE , 若DE∥BC , 则 =( )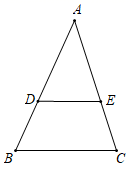 A、 B、 C、 D、5. 如图,在△ABC中,点D,E分别在边AB,AC上,且 ,则 的值为( )
A、 B、 C、 D、5. 如图,在△ABC中,点D,E分别在边AB,AC上,且 ,则 的值为( )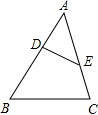 A、 B、1:2 C、1:3 D、1:46. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、 B、1:2 C、1:3 D、1:46. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、87. 如图,D、E、F分别是 各边中点,则以下说法错误的是( )
A、2 B、4 C、6 D、87. 如图,D、E、F分别是 各边中点,则以下说法错误的是( ) A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形8. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1 , 则点A1的坐标为( )
A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形8. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1 , 则点A1的坐标为( )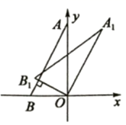 A、( ) B、( ) C、( ) D、( )9. 三个大小相同的等边三角形△ABC,△CDE,△GCF按如图所示方式摆放,点A, C, E在同一直线上,且点D,C,G在同一直线上,H为DE中点,以HB、HF为邻边作 BHFI,交AE于点M,N,若MN为8,则图中阴影部分的面积和为( )
A、( ) B、( ) C、( ) D、( )9. 三个大小相同的等边三角形△ABC,△CDE,△GCF按如图所示方式摆放,点A, C, E在同一直线上,且点D,C,G在同一直线上,H为DE中点,以HB、HF为邻边作 BHFI,交AE于点M,N,若MN为8,则图中阴影部分的面积和为( ) A、18 B、36 C、18 D、3610. 如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则 的值为( )
A、18 B、36 C、18 D、3610. 如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知△ABC的三边分别是5,6,7,则与它相似△ 的最短边为10,则△ 的周长是12. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 和 ,另一个三角形的最短边长为 ,则它的最长边为.13. 如图,在 中,D为BC上一点, ,则 的值为.
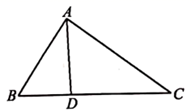 14. 如图,在△ABC中,AB=4,BC=5,点D、E分别在BC、AC上,CD=2BD,CF=2AF,BE交AD于点F,则△AFE面积的最大值是.
14. 如图,在△ABC中,AB=4,BC=5,点D、E分别在BC、AC上,CD=2BD,CF=2AF,BE交AD于点F,则△AFE面积的最大值是. 15. 如图,在 中, , , ,点E在线段 上,且 ,D是线段 上的一点,连接 ,将四边形 沿直线 翻折,得到四边形 ,当点G恰好落在线段 上时, .
15. 如图,在 中, , , ,点E在线段 上,且 ,D是线段 上的一点,连接 ,将四边形 沿直线 翻折,得到四边形 ,当点G恰好落在线段 上时, .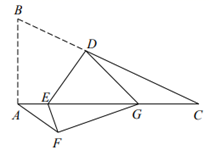
三、解答题
-
16. 如图,在平行四边形ABCD中,AB=3,AD= ,AF交BC于E,交DC的延长线于F,且CF=1,求CE的长
 17. 清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?
17. 清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点D)直行8里有一塔(点A),自西门(点E)直行2里至点B,切城角(点C)也可以看见塔,问这座方城每面城墙的长是多少里?

四、综合题
-
18. 如图,在 中, , cm, cm.点 是 边上的一动点,点 从点 出发以每秒2cm的速度沿 方向匀速运动,以 为边作等边 (点 、点在 同侧),设点 运动的时间为 秒, 与 重叠部分的面积为 .
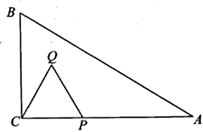 (1)、当点 落在 内部时,求此时 与 重叠部分的面积 (用含 的代数式表示,不要求写 的取值范围);(2)、当点 落在 上时,求此时 与 重叠部分的面积 的值:(3)、当点 落在 外部时,求此时 与 重叠部分的面积 (用含 的代数式表示).
(1)、当点 落在 内部时,求此时 与 重叠部分的面积 (用含 的代数式表示,不要求写 的取值范围);(2)、当点 落在 上时,求此时 与 重叠部分的面积 的值:(3)、当点 落在 外部时,求此时 与 重叠部分的面积 (用含 的代数式表示).