初中数学华师大版九年级上学期第23章 23.3.2 相似三角形的判定 同步练习
试卷更新日期:2021-08-03 类型:同步测试
一、单选题
-
1. 能判定 与 相似的条件是( )A、 B、 ,且 C、 且 D、 ,且2. 如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
 A、
A、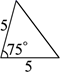 B、
B、 C、
C、 D、
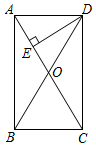
D、 3. 如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对( )
3. 如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对( ) A、6对 B、5对 C、4对 D、3对4. 如图,在 中, , , ,将 沿图示中的虚线 剪开,剪下的三角形与原三角形不相似的是( )
A、6对 B、5对 C、4对 D、3对4. 如图,在 中, , , ,将 沿图示中的虚线 剪开,剪下的三角形与原三角形不相似的是( )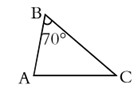 A、
A、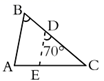 B、
B、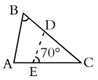 C、
C、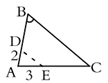 D、
D、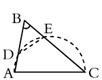 5. 下列命题是真命题的是( )A、同旁内角相等,两直线平行 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、两角分别相等的两个三角形相似6. 如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是( )
5. 下列命题是真命题的是( )A、同旁内角相等,两直线平行 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、两角分别相等的两个三角形相似6. 如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是( ) A、 B、 C、 D、7. 如图,点 在 的边 上,要判定 与 相似,需添加一个条件,则以下所添加的条件错误的是( )
A、 B、 C、 D、7. 如图,点 在 的边 上,要判定 与 相似,需添加一个条件,则以下所添加的条件错误的是( ) A、 B、 C、 D、8. 如图正方形网格上的三角形(1)(2)(3)中与△ABC相似的是( )
A、 B、 C、 D、8. 如图正方形网格上的三角形(1)(2)(3)中与△ABC相似的是( ) A、(1) B、(2) C、(3) D、都不与△ABC相似9. 如图,在 中, , , ,垂足为点 ,过点 作射线 ,点 是边 上任意一点,连接 并延长与射线 相交于点 ,设 , 两点之间的距离为 ,过点 作直线 的垂线,垂足为 .岑岑同学思考后给出了下面五条结论,正确的共有( )
A、(1) B、(2) C、(3) D、都不与△ABC相似9. 如图,在 中, , , ,垂足为点 ,过点 作射线 ,点 是边 上任意一点,连接 并延长与射线 相交于点 ,设 , 两点之间的距离为 ,过点 作直线 的垂线,垂足为 .岑岑同学思考后给出了下面五条结论,正确的共有( )① ;
②当 时, ;
③当 时,四边形 是平行四边形;
④当 或 时,都有 ;
⑤当 时, 与 一定相似.
 A、2条 B、3条 C、4条 D、5条
A、2条 B、3条 C、4条 D、5条二、填空题
-
10. 如图,要使△ACD∽△ABC,只需添加条件(只要写出一种合适的条件即可).
 11. 如图, , ,则图中相似三角形有对.
11. 如图, , ,则图中相似三角形有对. 12. 如图,在正方形网格中有3个斜三角形:① ;② ;③ ;其中能与 相似的是 . ( 除外)
12. 如图,在正方形网格中有3个斜三角形:① ;② ;③ ;其中能与 相似的是 . ( 除外) 13. 在 中, ,点P为 中点,经过点P的直线截 ,使截得的三角形与 相似,这样的直线共有条.14. 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形(图中阴影部分)的面积分别是S1=1,S2=4,S3=9,则△ABC的面积是
13. 在 中, ,点P为 中点,经过点P的直线截 ,使截得的三角形与 相似,这样的直线共有条.14. 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形(图中阴影部分)的面积分别是S1=1,S2=4,S3=9,则△ABC的面积是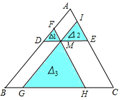 15. 如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t=时,△CPQ与△CBA相似.
15. 如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t=时,△CPQ与△CBA相似.
三、解答题