重庆市渝北区2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期：2021-08-03 类型：期中考试
一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卷上对应题目的正确答案标号涂黑）
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 计算a3•a2正确的是（ ）A、a B、a5 C、a6 D、a93. 如图，△ABC≌△CDE，且B、C、D三点共线，若AB＝4，DE＝3，则BD长为（ ）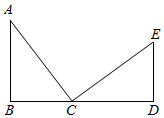
A、6 B、7 C、8 D、94. 若下列各组数值代表三根木棒的长度，则不能用它们摆成三角形的是（ ）A、3cm，4cm，5cm B、8cm，8cm，14cm C、6cm，7cm，11cm D、1cm，2cm，4cm5. 在平面直角坐标系中，点M（﹣3，2）关于y轴对称的点的坐标为（ ）A、（3，2） B、（3，﹣2） C、（﹣3，﹣2） D、（﹣3，2）6. 八边形的内角和为（ ）A、720° B、900° C、1080° D、1440°7. 下列说法：①三角形的一个外角大于它的任意一个内角；②三角形的三条高交于一点；③三角形的一条中线把三角形分成面积相等的两部分；④三角形的三条角平分线交于一点，该点到三角形三边距离相等.其中正确的个数有（ ）A、1个 B、2个 C、3个 D、4个8. 如图，在Rt△AED中，∠AED＝90°，∠EAD的角平分线交DE于F，过点F作FC⊥AD于C，点B为AE上一点，连接FB，且FB＝FD，AD＝6，AB＝3，则AC的长为（ ）
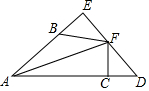A、3.5 B、4 C、4.5 D、59. 已知a﹣b＝﹣2，ab＝1，则a3b﹣2a2b2+ab3的值为（ ）A、﹣2 B、2 C、﹣4 D、410. 如图，将正方形（图①）作如下操作：第1次，分别连接各边中点，得到5个正方形（图②）；第2次将图②中左上角的正方形按上述方法再分割得到9个正方形（图③），…，以此类推，若要得到2033个正方形，则需要操作（ ）次.
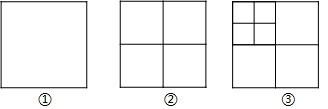A、506 B、507 C、508 D、50911. 若a2﹣b2＝16，（a+b）2＝8，则ab的值为（ ）A、﹣ B、 C、﹣6 D、612. 如图，点D、E、G分别为△ABC边AC、AB、BC上的点，连接DE、EG，将△ABC沿DE、EG翻折，顶点A，B均落在△ABC内部一点F处，且EA与EB重合于线段EF，若∠C＝54°，∠BGE＝66°；则∠ADE的度数为（ ）
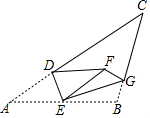A、77° B、78° C、79° D、80°二、填空题（本大题共6个小题，每小题4分，共24分请将答案写在答题卷上）
-
13. 因式分解：x3﹣9x= ．14. 如图，在△ABC中，线段BC的中垂线分别交边AB、BC于点D、点E，若△ADC的周长为9，且CE＝2，则△ABC的周长为.
15. 若一个等腰三角形的一个外角为160°，则该等腰三角形的底角的度数为.16. 已知2m＝5，22m+n＝45，则2n＝.17. 如图，长方形ABCD中，AB＝2，AD＝6，以点B为圆心，AB长为半径画圆交BC于点F，以点D为圆心，AD长为半径画圆交DC的延长线于点E，则图中阴影部分面积为.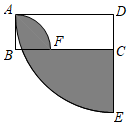
18. 因为新型冠状病毒引起的新冠肺炎是一种传染极强，传播速度极快，死亡率极高的急性感染性肺炎，所以政府号召市民保护好自己，勤洗手，戴口罩，市场上的口罩被一抢而空，为了缓解一罩难求的局面，政府要求各口罩生产企业加大力度生产口罩，我市的某棉纺企业立即改造了A、B、C三条生产线，加入到口罩生产的行列，第一周A、B、C三条生产线生产的口罩数量之比为6；4：7；第二周C生产线生产的口罩数量占第二周三条生产线生产的口罩总数量的 ，C生产线两周生产的口罩数量占三条生产线两周生产的口罩总数量的 ，而这两周A生产线生产的口罩总量与B生产线生产的口罩总量之比为24：17，那么B生产线两周生产的口罩数量与A、B、C三条生产线两周生产口罩总数量之比为.三、解答题（本大题共6个小题，每题10分共60分），解答时每小题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上
-
19. 计算下列各式(1)、 x（2x2y﹣3y）；(2)、（x+2y）（x﹣3y）+xy.20. 如图，在△ABC≌△DEC，点D在AB上，且AB∥CE，∠A＝75°，求∠DCB的度数.
21. 化简求值：[（x+y）（x﹣y）﹣（x﹣y）2]÷2y﹣y（4y﹣1），其中|x﹣3|+（y+ ）2＝0.22. 如图，在Rt△ABC中，点D为边AB上的一点，点F为线段AB延长线上一点，AD＝BF，AC＝DE且DE⊥EF，求证：∠ABC＝∠F.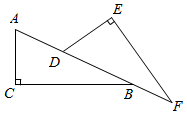
23. 在平面直角坐标系中，△ABC的各顶点坐标分别为（1，7），B（﹣2，4），C（2，2）.
(1)、利用关于坐标轴对称的点的坐标的特点，画出△ABC关于y轴对称的图形△A1B1C1 ， 并直接写出A1 ， B1 ， C1的坐标；(2)、若点D为x轴上一点，坐标为（d，0），且﹣2＜d＜2，若△B1C1D的面积为5，求点D的坐标.24. 斐波那契数列，又称黄金分割数列，因数学家斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0，1，1，2，3，5，8，…这个数列从第3项开始，每一项都等于前两项之和.而广义斐波那契数列指的是任意给定数列的前两项，这个数列从第3项开始，每一项都等于前两项之和例如：3，7，10，17，27，…(1)、斐波那契数列的第8项是 ， 第10项是；(2)、若一个广义斐波那契数列中间连续三项分别为75，m2 ， n2且m，n均为正整数，求m，n的值；(3)、已知x、y均为三位数，x＝ ，y＝ （其中a≠c分别为广义斐波那契数列的连续两项，且x的前一项能被8整除，求x，y的值.25. 已知：如图，△ABC和△CDE均为等腰三角形，AC＝BC，EC＝DC，BD⊥AD于点D，AD交BC于点F，点A、E、D三点共线，连接BD.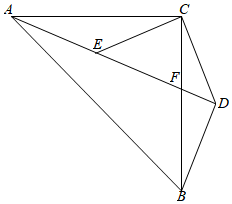
(1)、若∠ACE＝∠BCD，AD＝8，BD＝ AD，求DE的长；(2)、若∠ACB＝∠ECD＝90°，且BD＝CE，求证：BC＝AB﹣CF.26. 如图，在平面直角坐标系中，有Rt△ABC，∠ACB＝90°，∠BAC＝30°，点A、B均在x轴上，边AC与y轴交于点D，连接BD，且BD是∠ABC的角平分线，若点B的坐标为（ ，0）.
(1)、如图1，求点C的横坐标；(2)、如图2，将Rt△ABC绕点A逆时针旋转一个角度α（0°≤α≤180°）得到Rt△AB'C'，直线AC'交直线BD于点P，直线AB'交y轴于点Q，是否存在点P、Q，使△APQ为等腰三角形？若存在，直接写出∠APQ的度数；若不存在，请说明理由.