四川省成都市崇州市2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-08-03 类型：期中考试

进入出卷网下载

一、A卷选择题

1. 下列垃圾分类标识中，是中心对称图形的是（　　　）

A、 B、 C、 D、

查看试题解析
2. 下列四个等式从左到右的变形是因式分解的是（）

A、am+bm+c＝m （a+b）+c B、（2x+1）²＝4x²+4x+1 C、x²﹣1＝（x+1）（x﹣1） D、x²+x＝x² （1+ $\frac{1}{x}$ ）

查看试题解析
3. 使分式 $\frac{m - 1}{m - 3}$ 在实数范围内有意义，则实数m的取值范围是（　　）

A、m≠1 B、m≠3 C、m＝3 D、m＝1

查看试题解析
4. 已知三角形的三边长为a、b、c，如果 $\sqrt{a-5}$ +|b﹣12|+（c﹣13）²＝0，则△ABC是（　　）

A、以a为斜边的直角三角形 B、以b为斜边的直角三角形 C、以c为斜边的直角三角形 D、不是直角三角形

查看试题解析
5. 如图，在△ABC中，AB＝AC，AD为BC边上的中线，∠B＝25°，则∠BAD的度数为（　　）

A、55° B、65° C、75° D、85°

查看试题解析
6. 下列计算错误的是（　　）

A、 $\frac{{(a - b)}^{2}}{{(b - a)}^{2}}$ ＝1 B、 $\frac{x^{6}}{x^{2}} = x^{3}$ C、 $\frac{- a-b}{a+b}$ ＝﹣1 D、 $\frac{0.5 a + b}{0.2 a - 0.3 b} = \frac{5 a + 10 b}{2 a - 3 b}$

查看试题解析
7. 如图，电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求，发射塔到两个城镇M，N的距离必须相等，则发射塔应该建（）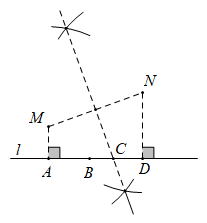

A、A处 B、B处 C、C处 D、D处

查看试题解析
8. 将点A（﹣2，﹣3）向左平移3个单位，再向上平移4个单位得到点B，则点B的坐标是（　　）

A、（﹣5，﹣7） B、（﹣5，1） C、（1，1） D、（1，﹣7）

查看试题解析
9. 如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB交BC于D，DE⊥AB于E.若DE＝1cm，则BC＝（　　）cm.

A、2 B、3 C、4 D、5

查看试题解析
10. 5G是未来社会的基础设施，是国家战略.5G网络峰值速率是4G网络峰值速率的10倍，在峰值速率下传输1000兆数据，5G网络比4G网络快约90秒，求这两种网络的峰值速率，设4G网络的峰值速率为每秒传输x兆数据，依题意，可列方程是（　　）

A、 $\frac{1000}{x} - \frac{1000}{10 x}$ ＝90 B、 $\frac{1000}{10 x} - \frac{1000}{x}$ ＝90 C、 $\frac{10000}{x} - \frac{1000}{x}$ ＝90 D、 $\frac{1000}{x} - \frac{10000}{x}$ ＝90

查看试题解析

二、填空题。（本大题共4个小题，每小题0分，共16分）

11. 如果x²+Ax+B因式分解的结果为（x﹣3）（x+5），则A＝， B＝.

查看试题解析
12. x²﹣mx+9是完全平方式，则m＝．

查看试题解析
13. 老师在投影屏上展示了如下一道试题：
已知：如图，BD平分∠ABC，AB＝AD.求证：AD∥BC.

证明：∵BD平分∠ABC，

∴∠ABD＝∠CBD（①角平分线定义）.

∵AB＝AD，

∴∠ABD＝∠ADB（②等角对等边）.

∴③∠ADB＝∠DBC，

∴AD∥BC（④内错角相等，两直线平行）.

则以上证明过程中，结论或者依据错误的一项是.

查看试题解析
14. 如图，将Rt△ABC（∠BAC＝65°）绕点A顺时针旋转到△AB₁C₁的位置，使得点C，A，B₁在同一直线上，则旋转角度为.

查看试题解析

三、三.解答题

15. 把下列各题因式分解：

(1)、mn（n﹣m）﹣n（m﹣n）；

(2)、2x²y﹣8xy+8y.

查看试题解析
16. 解答下列各题

(1)、 $\frac{4 a}{3 b} \cdot \frac{b}{2 a^{4}} \div {(\frac{1}{a})}^{2}$ ；

(2)、先化简，再求值： $\frac{a^{2} + a}{a^{2} - 2 a + 1} \div (\frac{2 a}{a - 1} - 1)$ ，其中a＝3.

查看试题解析
17. 解下列方程.

(1)、 $\frac{1}{2 x + 1} = \frac{2}{x}$ ；

(2)、 $\frac{x}{x + 2} + \frac{3}{x - 3} = 1$ .

查看试题解析
18. 如图，在平面直角坐标系中，Rt△ABC三个顶点都在格点上，点A、B、C的坐标分别为A（﹣4，1），B（﹣1，1），C（﹣1，3）请解答下列问题：

（ 1 ）△ABC与△A₁B₁C₁关于原点O成中心对称，画出△A₁B₁C₁并直接写出点C的对应点C₁的坐标；

（ 2 ）画出△ABC绕原点O逆时针旋转90°后得到的△A₂B₂C₂ ，并求出点A旋转至A₂经过的路径长.

查看试题解析
19. 如图，在△ABC中，∠A＝90°，∠B＝30°，AC＝6厘米，点D从点A开始以1厘米/秒的速度向点C运动，点E从点C开始以2厘米/秒的速度向点B运动，两点同时运动，同时停止，运动时间为t秒；过点E作EF∥AC交AB于点F；

(1)、当t为何值时，△DEC为等边三角形？

(2)、当t为何值时，△DEC为直角三角形？

(3)、求证：DC＝EF.

查看试题解析

四、四.B卷填空。

20. 已知关于x，y的二元一次方程组 ${\begin{cases} a x + b y = 1 \\ a y + b x = 5 \end{cases}$ 的解是 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ ，则a²﹣b²＝.

查看试题解析
21. 对于实数a、b，定义一种新运算“⊗”为：a⊗b= $\frac{1}{a - b^{2}}$ ，这里等式右边是实数运算．例如：1⊗3= $\frac{1}{1 - 3^{2}}$ =﹣ $\frac{1}{8}$ ．则方程x⊗（﹣2）= $\frac{2}{x - 4}$ ﹣1的解是．

查看试题解析
22. 若关于x的方程 $\frac{x - 1}{x - 5} = \frac{m}{10 - 2 x}$ 无解，则m＝.

查看试题解析
23. 如图，已知∠MON＝30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形，若OA₁＝1，则△A₂₀₂₀B₂₀₂₀A₂₀₂₁的边长为.

查看试题解析
24. 如图，△ABC是等边三角形，且AB＝1，点M为直线BC上的一个动点，连接AM，将线段AM绕A点顺时针旋转60°至AD，点N为直线AC上的一个动点，则D、N两点间距离的最小值为.

查看试题解析

五、五.B卷解答题.

25. 对于两个不等的非零实数a，b，若分式 $\frac{(x - a) (x - b)}{x}$ 的值为0，则x＝a或x＝b.
因为 $\frac{(x - a) (x - b)}{x} = \frac{x^{2} - (a + b) x + a b}{x} = x + \frac{a b}{x} - (a + b)$ ，所以关于x的方程x+ $\frac{ab}{x}$ ＝a+b的两个解分别为x₁＝a，x₂＝b.

利用上面建构的模型，解决下列问题：

(1)、若方程x+ $\frac{p}{x}$ ＝q的两个解分别为x₁＝﹣1，x₂＝4.则p＝， q＝；（直接写出结论）

(2)、已知关于x的方程2x+ $\frac{n^{2} + n - 2}{2 x + 1}$ ＝2n的两个解分别为x₁ ， x₂（x₁＜x₂）.求 $\frac{2 x_{1}}{2 x_{2} - 3}$ 的值.

查看试题解析
26.

(1)、【问题原型】如图1，在等腰直角三角形ABC中，∠ACB＝90°，BC＝8.将边AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D作△BCD的BC边上的高DE，易证△ABC≌△BDE，从而得到△BCD的面积为.

(2)、【初步探究】如图2，在Rt△ABC中，∠ACB＝90°，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD.用含a的代数式表示△BCD的面积并说明理由.

(3)、【简单应用】如图3，在等腰三角形ABC中，AB＝AC，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，求△BCD的面积（用含a的代数式表示）.

查看试题解析
27. 如图1，已知点B（0，6），点C为x轴上一动点，连接BC，△ODC和△EBC都是等边三角形.

(1)、求证：DE＝BO；

(2)、如图2，当点D恰好落在BC上时.
①求OC的长及点E的坐标；

②在x轴上是否存在点P，使△PEC为等腰三角形？若存在，写出点P的坐标；若不存在，说明理由；

③如图3，点M是线段BC上的动点（点B，C除外），过点M作MG⊥BE于点G，MH⊥CE于点H，当点M运动时，MH+MG的值是否发生变化？简要说明理由.

查看试题解析