湖南省长沙市开福区2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-08-03 类型：期中考试

进入出卷网下载

一、单选题（每小题3分，共36分）

1. 下列函数中，y是x的一次函数的是（）

A、y=﹣3x+5 B、y=﹣3x² C、y= $\frac{1}{x}$ D、y=2 $\sqrt{x}$

查看试题解析
2. 直角三角形中，两直角边分别是12和5，则斜边上的中线长是（　　）

A、34 B、26 C、8.5 D、6.5

查看试题解析
3. 菱形的两条对角线长分别为9cm和4cm，则此菱形的面积是（　　）

A、16cm² B、4 $\sqrt{13}$ cm² C、18cm² D、2 $\sqrt{13}$ cm²

查看试题解析
4. 关于函数y=﹣2x+1，下列结论正确的是（　　）

A、图象必经过（﹣2，1） B、y随x的增大而增大 C、图象经过第一、二、三象限 D、当x＞ $\frac{1}{2}$ 时，y＜0

查看试题解析
5. 下列说法不正确的是（）

A、有两组对边分别平行的四边形是平行四边形 B、平行四边形的对角线互相平分 C、平行四边形的对边平行且相等 D、平行四边形的对角互补，邻角相等

查看试题解析
6. 将直线y=﹣7x+4向下平移3个单位长度后得到的直线的表达式是（）

A、y=﹣7x+7 B、y=﹣7x+1 C、y=﹣7x﹣17 D、y=﹣7x+25

查看试题解析
7. 矩形的四边中点所组成的四边形是（　　）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
8. 点（a，﹣1）在一次函数y＝﹣2x+1的图象上，则a的值为（　　）

A、a＝﹣3 B、a＝﹣1 C、a＝1 D、a＝2

查看试题解析
9. 如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y轴上，则点C的坐标是（）

A、（4，5） B、（5，4） C、（4，4） D、（5，3）

查看试题解析
10. 某同学从家骑自行车上学，先上坡到达A地后再下坡到达学校，所用的时间与行驶的路程如图所示，如果返程上、下坡速度保持不变，那么他从学校回到家需要的时间是（）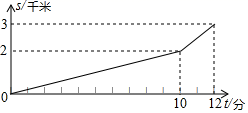

A、14分钟 B、12分钟 C、9分钟 D、7分钟

查看试题解析
11. 如图，已知函数y＝x+1和y＝ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组 ${\begin{cases} x - y = 1 \\ a x - y = - 3 \end{cases}$ 的解是（　　）

A、 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ B、 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ C、 ${\begin{cases} x = 1 \\ y = - 2 \end{cases}$ D、 ${\begin{cases} x = - 2 \\ y = 1 \end{cases}$

查看试题解析
12. 如图，D，E分别是AB，AC上的中点，F是DE上的一点，且∠AFB＝90°，若AB＝6，BC＝8，则EF的长为（　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每小题3分，共18分）

13. 如图，矩形ABCD的对角线AC、BD相交于点O，∠AOD＝120°，AB＝4cm，则矩形的对角线长为.

查看试题解析
14. 已知一次函数y＝kx+b的图象如图所示，当y＜0时，x的取值范围是.

查看试题解析
15. 如图，在平行四边形ABCD中，AC⊥BC，AD＝AC＝4，则BD的长为.

查看试题解析
16. 直线y＝4x﹣4与坐标轴所围成的三角形面积为.

查看试题解析
17. 如图，在正方形 $A B C D$ 的外侧，作等边 $△ D C E$ ，则 $∠ A E C$ 的度数是．

查看试题解析
18. 已知直线y＝（m﹣5）x+m﹣4不经过第三象限，则m的取值范围是．

查看试题解析

三、解答题（共8题，共66分）

19. 计算： $| - \sqrt{3} + 1 | - {(2021 - π)}^{0} + \sqrt[3]{- 8}$ .

查看试题解析
20. 先化简，后求值： $(\frac{x}{x - 2} - \frac{4}{x^{2} - 2 x}) \div \frac{x + 2}{x^{2} - x}$ ，其中x为整数且满足﹣2＜x＜3.

查看试题解析
21. 如图，▱ABCD的对角线AC、BD相交于点O，EF过点O且与AB、CD分别相交于点E、F，连接EC.

(1)、求证：OE＝OF；

(2)、若EF⊥AC，△BEC的周长是10，求▱ABCD的周长.

查看试题解析
22. 已知一次函数y＝kx+b，当1≤x≤4时，3≤y≤6，求 $\frac{b}{k}$ 的值.

查看试题解析
23. 如图，在矩形ABCD中，AB＝8cm，BC＝16cm，点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．

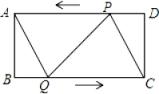(1)、当t为何值时，四边形ABQP是矩形；

(2)、当t为何值时，四边形AQCP是菱形；

(3)、分别求出(2)中菱形AQCP的周长和面积．

查看试题解析
24. 一次函数y＝（2m+1）x+m﹣3

(1)、若函数图象经过原点，求m的值

(2)、若函数图象平行于直线y＝3x﹣3，求m的值：

(3)、在（1）的条件下，将这个正比例函数的图象向右平移4个单位，求出平移后的直线解析式.

查看试题解析
25. 通程电器商城购3台空调、2台彩电需花费2.32万元.购2台空调、4台彩电需，花费2.48万元.

(1)、计算每台空调与彩电的进价分别是多少元？

(2)、已知一次性购进空调、彩电共30台，购进资金不超过12.8万元，购进空调不少于10台，写出符合要求的进货方案；

(3)、在（2）的情况下，原每台空调的售价为6100元.每台彩电的售价为3900元，根据市场需要，商城举行“庆五一优惠活动”，每台空调让利a元（0＜a＜350），设商城计划购进空调x台，空调和彩电全部销售完商城获得的利润为y元.试写出y与x的函数关系式，选择哪种进货方案，商城获利最大？

查看试题解析
26. 若两个一次函数与x轴的交点关于y轴对称，则称这两个一次函数为“对心函数”，这两个与x轴的交点为“对心点”.如：y＝x+3与x轴的交点是（﹣3，0）；y＝﹣x+3与x轴的交点是（3，0），则y＝x+3是y＝﹣x+3的对心函数；这两个对心点为（﹣3，0）和（3，0）.

(1)、写出一个y＝2x+6的对心函数：，这两个“对心点”为；

(2)、直线l₁ ，经过点A（﹣1，0）和B（0，﹣3），直线l₁的“对心函数”直线l₂与y轴的交点D位于点（0，1）的上方，且直线l₁与直线l₂交于点E，点C为直线l₂的“对心点”，点G是动直线l₂上不与C重合的一个动点，且BG＝BA，试探究∠ABG与∠ECA之间的数量关系，并说明理由；

(3)、如图，直线l₃：y＝x+2与其“对心函数”直线l₄的交点F位于第一象限，M、N分别为直线l₃、l₄的“对心点”，点P为线段MF上一点（不含端点），连接NP；一动点H从N出发，沿线段NP以1单位/秒的速度运动到点P，再沿线段PF以 $\sqrt{2}$ 单位/秒的速度运动到点F后停止，点H在整个运动过程中所用最短时间为6秒，求直线l₄的解析式.

查看试题解析