甘肃省张掖市甘州区2020-2021学年八年级下学期数学期中考试试卷B

试卷更新日期：2021-08-03 类型：期中考试

进入出卷网下载

一、一.选择题

1. 下列x的值不是不等式﹣2x+4＜0的解，答案是（　　）

A、﹣2 B、3 C、3.5 D、10

查看试题解析
2. 直角三角形的两条直角边分别为5cm，12cm，则斜边上的高是（　　）cm.

A、6 B、8 C、 $\frac{90}{13}$ D、 $\frac{60}{13}$

查看试题解析
3. 已知x＞y，那么下列不等式成立的是（　　）

A、x﹣6＜y﹣6 B、3x＜3y C、﹣2x＜﹣2y D、﹣x＞﹣y

查看试题解析
4. 下列说法不正确的是（　　）

A、平行四边形对边平行 B、两组对边平行的四边形是平行四边形 C、平行四边形对角相等 D、一组对角相等的四边形是平行四边形

查看试题解析
5. 等腰三角形一腰上的高与另一腰的夹角是50°，则这个等腰三角形的底角为（）

A、70° B、20° C、70°或20° D、40°或140°

查看试题解析
6. 一次智力测验，有20道选择题．评分标准是：对1题给5分，错1题扣2分，不答题不给分也不扣分．小明有两道题未答．至少答对几道题，总分才不会低于60分．则小明至少答对的题数是（）

A、11道 B、12道 C、13道 D、14道

查看试题解析
7. 如图，在△ABC中，∠C＝90°，AC＝8，DC＝ $\frac{1}{3}$ AD，BD平分∠ABC，则点D到AB的距离等于（　　）

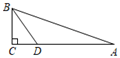A、4 B、3 C、2 D、1

查看试题解析
8. 如图，在▱ABCD中，已知AC＝4cm，若△ACD的周长为13cm，则▱ABCD的周长为（　　）

A、26cm B、24cm C、20cm D、18cm

查看试题解析
9. 如图，一次函数y₁＝k₁x+b与一次函数y₂＝k₂x+4的图象交于点P（1，3），则关于x的不等式k₁x+b＞k₂x+4的解集是（　　）

A、x＞1 B、x＞0 C、x＞﹣2 D、x＜1

查看试题解析
10. 如图，已知AB＝AC，∠A＝36°，AB的垂直平分线MD交AC于D，AB于M，以下结论：①△BCD是等腰三角形；②射线BD是△ACB的角平分线；③△BCD的周长C_△_BCD＝AC+BC；④△ADM≌△BCD.正确的有（　　）

A、①② B、①③ C、①②③ D、③④

查看试题解析

二、二.填空题

11. 不等式9﹣3x＞0的非负整数解有个.

查看试题解析
12. 在平行四边形ABCD中，已知∠A﹣∠B＝60°，则∠C＝.

查看试题解析
13. 等腰三角形的周长为14，其一边长为4，那么它的底边为.

查看试题解析
14. 若一个多边形的内角和等于它的外角和，则这个多边形的边数为.

查看试题解析
15. 当k时，代数式 $\frac{2}{3}$ （k﹣1）的值不小于代数式1﹣ $\frac{5 k - 1}{6}$ 的值．

查看试题解析
16. 如图，已知在△ABC中，DE是BC的垂直平分线，垂足为E，交AC于点D，若AB＝6，AC＝9，则△ABD的周长是.

查看试题解析
17. 如图，△ABC的三边AB，CA，BC的长分别为40，50，60，其三条角平分线交于点O，则S_△_ABO：S_△_BCO：S_△_CAO＝.

查看试题解析
18. 如图，在▱ABCD中，AB＝8cm，BC＝16cm，∠A＝60°.点E从点D出发沿DA边运动到点A，点F从点B出发沿BC边向点C运动，点E运动速度为2cm/s，点F的运动速度为1cm/s，它们同时出发，同时停止运动，经过s时，EF＝AB.

查看试题解析

三、三.解答题

19. 如图，OA、OB表示两条相交的公路，点M、N是两个工厂，现在要在∠AOB内建立一个货物中转站P，使中转站到公路OA、OB的距离相等，并且到工厂M、N的距离也相等，用尺规作出货物中转站P的位置.

查看试题解析
20. 如图，直线m和直线l表示两条公路，A，B表示两个村庄.现在要建一个交通中转站P，并使P到A，B两个村庄的距离相等，到公路m，l的距离相等.确定中转站P的位置，并用直尺和圆规作出图形.

查看试题解析
21. 解下列不等式组，并把它们的解集在数轴上表示出来：

(1)、 ${\begin{cases} 1 + 2 x < 3 x + 2 \\ x - 3 \leq 3 (x + 5) \end{cases}$

(2)、 ${\begin{cases} 6 x - 2 \geq 3 x - 4 \\ \frac{2 x + 1}{3} - \frac{1 - x}{2} < 1 \end{cases}$

(3)、 ${\begin{cases} 2 x + 5 \leq 3 (x + 2) \\ \frac{x - 1}{3} < \frac{x - 2}{2} \end{cases}$

(4)、 ${\begin{cases} 2 x - 7 < 3 (1 - x) \\ \frac{4}{3} + 3 \leq 1 - \frac{2}{3} x \end{cases}$ .

查看试题解析
22. 如图，点C是AB的中点，AD＝CE，CD＝BE.

(1)、求证：△ACD≌△CBE；

(2)、连接DE，求证：四边形CBED是平行四边形.

查看试题解析
23. 已知关于x的方程 $\frac{x + m}{3} - \frac{2 x - 1}{2}$ ＝m的解为负数，求m的取值范围.

查看试题解析
24. 如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC.

(1)、求∠BEC的度数.

(2)、若AE＝5，求BC的长.

查看试题解析
25. 如图，树AB垂直于地面，为测树高，小明在C处，测得∠ACB＝15°，他沿CB方向走了20米，到达D处，测得∠ADB＝30°，你能帮助小明计算出树的高度吗？

查看试题解析
26. 如图，▱ABCD中，点E、F在BD上，且BF＝DE.

(1)、写出图中所有你认为全等的三角形；

(2)、连接AF、CE，四边形AFCE是平行四边形吗？请证明你的结论.

查看试题解析
27. 如图，四边形ABCD中，对角线AC，BD相交于点O，AB＝AC＝AD，∠DAC＝∠ABC.

(1)、求证：BD平分∠ABC；

(2)、若∠DAC＝45°，OA＝1，求OC的长.

查看试题解析
28. 五一节快到了，甲、乙两家旅行社为了吸引更多的顾客，分别提出了赴某地旅游的团体优惠方法，甲旅行社的优惠方法是：买4张全票，其余人按半价优惠；乙旅行社的优惠方法是：一律按7折优惠，已知两家旅行社的原价均为每人100元．（旅游人数超过4人）

(1)、分别表示出甲旅行社收费y₁ ，乙旅行社收费y₂与旅游人数x的函数关系式．

(2)、就参加旅游的人数讨论哪家旅行社的收费更优惠？

查看试题解析
29. 以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE，连接EB、FD，交点为G.

(1)、当四边形ABCD为正方形时（如图1），EB和FD的数量关系是；

(2)、当四边形ABCD为矩形时（如图2），EB和FD具有怎样的数量关系？请加以证明；

(3)、四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请说明理由；如果不变，请在图3中求出∠EGD的度数.

查看试题解析