甘肃省张掖市甘州区2020-2021学年八年级下学期数学期中考试试卷A
试卷更新日期：2021-08-03 类型：期中考试
一、一.选择题（共10小题，30分）
-
1. 已知a＜b，下列四个不等式中正确的是（ ）A、3a＞3b B、﹣a＜﹣b C、a+3＜b+3 D、a﹣6＞b﹣62. 在平面直角坐标系中，点P（﹣1，2）向上平移3个单位长度后的坐标是（ ）A、（2，2） B、（﹣4，2） C、（﹣1，5） D、（﹣1，﹣1）3. 下列图案中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
4. 不等式﹣2x+5≥1的解集在数轴上表示正确的是（ ）A、
B、
C、
D、
5. 等腰三角形的一边为4，另一边为9，则这个三角形的周长为（ ）A、17 B、22 C、13 D、17或226. 如图，已知∠ADB＝∠ADC，则不一定能使△ABD≌△ACD的条件是（ ）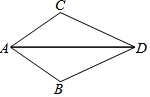
A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠BAD＝∠CAD7. 不等式2x+1＜8的最大正整数解是（ ）A、1 B、2 C、3 D、48. 如图，将△AOB绕点O按逆时针方向旋转55°后得到△A′OB′，若∠AOB＝15°，则∠AOB′的度数是（ ）
A、25° B、30° C、35° D、40°9. 如图，在△ABC中，AB＝AC，DE垂直平分AB，分别交AB、AC于点D、E，若∠EBC＝30°，则∠A＝（ ）
A、30° B、35° C、40° D、45°10. 如图，△ABC中，DE是AC的垂直平分线，AE＝5cm，△ABD的周长为18cm，则△ABC的周长为（ ）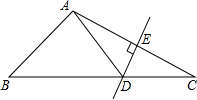
A、23cm B、28cm C、13cm D、18cm二、二.填空题（共8小题，32分）
-
11. 一个等腰三角形的一个角为80°，则它的顶角的度数是 ．
12. 如果y＝2x﹣5，那么当y＜0时，x .（填写“＞”或“＜”号）13. 已知直角三角形中30°角所对的直角边长是2cm，则斜边的长是.14. 如图，△ABC沿BC方向平移到△DEF的位置，若BE＝2cm，则CF＝.
15. 如图，在3×3的网格中，每个网格线的交点称为格点.已知图中A，B两个格点，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的点C有个.
16. 如图，将Rt△ABC（其中∠B＝35°，∠C＝90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角的度数是.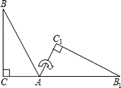
17.边长为1的一个正方形和一个等边三角形如图摆放，则△ABC的面积为 .
18. 如图所示，在△ABC中，∠A＝90°，BD是∠ABC的平分线，DE是BC的垂直平分线，则∠C＝.
三、三.解答题（共9小题，88分）
-
19.(1)、解不等式 ，并把它的解集在数轴上表示出来.(2)、解不等式组 ，并写出它的整数解.20. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：
（ 1 ）画出△ABC关于x轴对称的△A1B1C1 ， 并写出点A1的坐标.
（ 2 ）画出△A1B1C1绕原点O中心对称的△A2B2C2 ， 并写出点A2的坐标.
21. 如图，在△ABC中，AD是它的角平分线，且BD＝CD，DE⊥AB，DF⊥AC，垂足分别为E，F.求证：EB＝FC.
22. 燃放某种礼花弹时，为了确保安全，人在点燃导火线后要在燃放前转移到10m外的安全区域，已知导火线的燃烧速度为0.02m/s，人离开的速度为4m/s，那么导火线的长度至少应为多少米？23. 如图，在△ABC中，∠C＝90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．
(1)、求证：△ACD≌△AED；(2)、若∠B＝30°，CD＝1，求BD的长．24. 如图，在△ABC中，AB的垂直平分线MN交AB于点E，交AC于点D，且AC＝15cm，△BCD的周长等于25cm.
(1)、求BC的长；(2)、若∠A＝36°，并且AB＝AC，求证：BC＝BD.25. 用若干辆载重量为8吨的汽车运一批货物，若每辆汽车只装4吨，则剩下20吨货物；若每辆汽车装满8吨，则最后一辆汽车不满也不空，请问有多少辆汽车？26. 某校张老师暑假准备带领他们的“三好学生”外出旅游，甲、乙两家旅行社的服务质量相同，且报价都是每人400元，经协商，甲旅行社表示：“如果带队张老师买一张全票，则学生可半价”；乙旅行社表示：“所有游客全部享受6折优惠.”则：(1)、设学生数为x（人），甲旅行社收费为y甲（元），乙旅行社收费为y乙（元），两家旅行社的收费各是多少？(2)、哪家旅行社收费较为优惠？27. 已知：点O在直线AB上，OD平分∠AOC，OE平分∠BOC.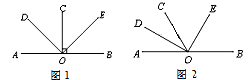
(1)、若OC⊥AB于点O，如图1，直接写出∠DOE的度数为；OD与OE的位置关系是；(2)、若OC与AB不垂直，如图2，其它条件不变，（1）中的结论还成立吗？若成立，请说明你的猜想是正确的；若不成立，请说明理由；(3)、如图2，若∠AOD＝40°，请你利用（2）中得到的结论，求∠BOE的度数．