浙江省宁波市鄞州区横溪、东吴、咸祥等2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期：2021-08-03 类型：期中考试
一、选择题（每小题3分，共30分。在每小题给出的四个选项中，只有一项符合题目要求）
-
1. 下列是有关防疫的图片，其中是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列方程是一元二次方程的是（ ）A、x2﹣5x＝1 B、3x+2y＝1 C、x2﹣ ＝1 D、ax2﹣3x+1＝03. 若 ＝3﹣x成立，则x满足的条件是（ ）A、x≥3 B、x≤3 C、x＞3 D、x＜34. 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：尺码
39
40
41
42
43
平均每天销售数量（件）
10
12
20
12
12
该店主决定本周进货时，增加了一些41码的衬衫，影响该店主决策的统计量是（ ）
A、众数 B、方差 C、平均数 D、中位数5. 用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（ ）A、有一个内角小于90° B、每一个内角都大于90° C、有一个内角小于或等于90° D、每一个内角都小于90°6. 方程（x+3）2＝4的根是（ ）A、x1＝﹣1，x2＝﹣5 B、x1＝1，x2＝﹣5 C、x1＝x2＝﹣1 D、x1＝﹣1，x2＝57. 在四边形ABCD中，对角线AC与BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）A、AB∥DC，AD∥BC B、AD∥BC，AB＝DC C、AB∥DC，∠DAB＝∠DCB D、AO＝CO，BO＝DO8. 某班部分学生上学路上所花的时间被绘制成如图所示的频数分布直方图，设他们上学路上所花的时间的平均数为a，中位数为b，众数为c，则a，b，c的大小关系为（ ）
A、a＞b＞c B、b＞a＞c C、b＞c＞a D、c＞a＞b9. 有1人患了流感，经过两轮传染后共有81人患了流感，设每轮传染中每人传染x人，其中20%的人因自身抵抗力强而未患流感，则根据题意可列方程为（ ）A、0.2（1+x）2＝81 B、（1+0.2x）2＝81 C、0.8（1+x）2＝81 D、（1+0.8x）2＝8110. 如图，在▱ABCD中，过点A分别作AE⊥BC于点E，AF⊥CD于点F，分别作点C关于AB，AD的对称点G，H，连接CG，CH，AG，AH，GH.如果AB＝30，∠EAF＝30°，▱ABCD的面积为270 ，那么下列说法不正确的是（ ）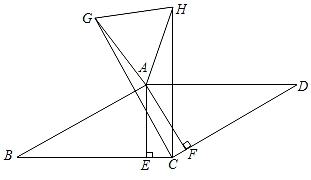
A、CE＝ CF B、∠GAH＝60° C、GH＝AF+CF D、△GCH的面积是▱ABCD的面积的一半二、填空题（每小题3分，共18分）
-
11. 在二次根式 中，字母a的取值范围为.12. 已知正n边形的每个内角为144°，则n＝.13. 若x＝﹣1是关于x的一元二次方程x2﹣3x﹣2p＝0的一个根，则p＝.14. 实数 的整数部分为.15. 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S2 ， 那么数据a+99，b+100，c+101的方差将 S2（填“大于”“小于”或“等于”）.16. 如图，△ABC和△DBC均在BC的上方，边AC与BD相交于一点，M是BD的中点，N是AC的中点，连接MN.若AB＝4 ，CD＝4，MN＝2，∠BCD＝80°，则∠ABC＝ .
三、解答题（本大题有7小题，共52分）
-
17.(1)、计算： ；(2)、已知m＝ ﹣2，求代数式m2+4m的值.18. 解方程：(1)、x（2x﹣5）＝2x﹣5；(2)、x2﹣2x﹣1＝0.19. 为了在甲、乙两名学生中选择一人去参加数学竞赛，李老师统计了他们两人5次的模拟考试成绩，并绘制成不完整的折线统计图.已知他们两人这5次模拟考试的总成绩相同，请你解答下列问题：
(1)、求a的值和乙的成绩的平均数；(2)、请补全乙的模拟考试成绩的折线图；(3)、已知甲成绩的方差是360分2 ， 请计算乙成绩的方差，并从平均数和方差的角度分析，李老师应该选择哪名学生去参加数学竞赛.甲、乙两人模拟考试成绩统计表：
甲成绩（分）
乙成绩（分）
第1次
90
70
第2次
40
50
第3次
70
70
第4次
40
a
第5次
60
70
20. 已知关于x的方程mx2﹣（m+2）x+2＝0.(1)、证明：不论m为何值时，方程总有实数根；(2)、m为何整数时，方程有两个不相等的正整数根.21. 如图，在▱ABCD中，F是AD的中点，延长BC到点E，使CE＝ BC，连接DE，CF.
(1)、求证：四边形CEDF是平行四边形；(2)、若AB＝4，AD＝6，∠B＝60°，求DE的长.22. 在“精准扶贫”工作中，某单位建议贫困户借助家里长25m的墙AB建造面积为450m2的长方形区域来养一些家禽，该单位给贫困户提供65m长的篱笆（全部用于建造长方形区域），并提供如图所示的两种方案：
(1)、如图1，若选取墙AB的一部分作为长方形的一边，其他三边用篱笆围成，则在墙AB上借用的CF的长度为多少？(2)、如图2，若将墙AB全部借用，并在墙AB的延长线上拓展BF，构成长方形ADEF，BF，FE，ED和DA都由篱笆构成，求BF的长.23. 我们把能平分一个图形面积的直线称为该图形的“好线”.如图1，三角形的中线所在直线就是该三角形的一条好线.
(1)、平行四边形的好线共有条；(2)、如图2，四边形ABCD中，取对角线BD的中点O，连接OA、OC，再过点O作OE∥AC交CD于E，连接AE.证明：直线AE是四边形ABCD的“好线”；(3)、如图3，AE为一条“好线”，F为AD边的一点，请作出经过F点的一条“好线”，并说明哪条直线是四边形ABCD的“好线”（不擦除作图痕迹，无需说明理由）.