陕西省西安市蓝田县2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2021-08-03 类型:期中考试
一、选择题(共10小题,每小题3分,计30分.)
-
1. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、
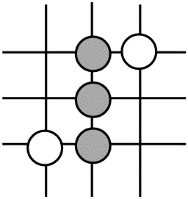
B、
B、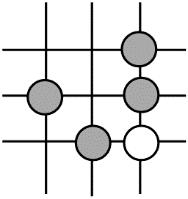
C、
C、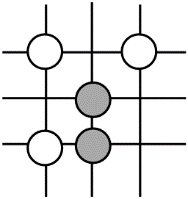
D、
D、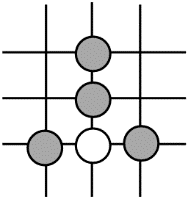
2. 用反证法证明“a≥b”时应先假设( )A、a≤b B、a>b C、a<b D、a≠b3. 下列各式从左到右的变形中,属于因式分解的是( )A、a(m+n)=am+an B、x2﹣16+6x=(x+4)(x﹣4)+6x C、x2+2x﹣1=(x﹣1)2﹣2 D、x2﹣25=(x+5)(x﹣5)4. 若m>n,则下列不等式一定成立的是( )A、2m<3n B、3+m>3+n C、1﹣m>1﹣n D、 <5. 在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )A、(3,1) B、(3,3) C、(﹣1,1) D、(﹣1,3)6. 如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为( )
2. 用反证法证明“a≥b”时应先假设( )A、a≤b B、a>b C、a<b D、a≠b3. 下列各式从左到右的变形中,属于因式分解的是( )A、a(m+n)=am+an B、x2﹣16+6x=(x+4)(x﹣4)+6x C、x2+2x﹣1=(x﹣1)2﹣2 D、x2﹣25=(x+5)(x﹣5)4. 若m>n,则下列不等式一定成立的是( )A、2m<3n B、3+m>3+n C、1﹣m>1﹣n D、 <5. 在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )A、(3,1) B、(3,3) C、(﹣1,1) D、(﹣1,3)6. 如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为( )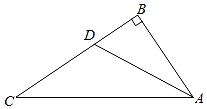 A、4 B、6 C、8 D、107. 如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b>0的解集是( )
A、4 B、6 C、8 D、107. 如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b>0的解集是( )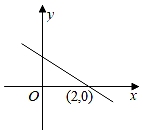 A、x>2 B、x<2 C、x≥2 D、x≤28. 如图,将△ABC绕点A顺时针旋转得到△ADE,且点D恰好在AC上,∠BAE=∠CDE=136°,则∠C的度数是( )
A、x>2 B、x<2 C、x≥2 D、x≤28. 如图,将△ABC绕点A顺时针旋转得到△ADE,且点D恰好在AC上,∠BAE=∠CDE=136°,则∠C的度数是( ) A、24° B、26° C、30° D、36°9. 如图,已知△ABC与△CDA关于点O中心对称,过点O任作直线分别交AD、BC于点M、N,下列结论:①点M和点N,点B和点D分别关于点O对称;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DMOC和四边形BNOA的面积相等;⑤△AOM和△CON成中心对称.其中正确的有( )
A、24° B、26° C、30° D、36°9. 如图,已知△ABC与△CDA关于点O中心对称,过点O任作直线分别交AD、BC于点M、N,下列结论:①点M和点N,点B和点D分别关于点O对称;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DMOC和四边形BNOA的面积相等;⑤△AOM和△CON成中心对称.其中正确的有( ) A、2个 B、3个 C、4个 D、5个10. 若关于 x 的不等式组 恰好只有 2 个整数解,则所有满足条件的整数 a 的值之和是( )A、3 B、4 C、6 D、1
A、2个 B、3个 C、4个 D、5个10. 若关于 x 的不等式组 恰好只有 2 个整数解,则所有满足条件的整数 a 的值之和是( )A、3 B、4 C、6 D、1二、填空题(共4小题,每小题3分,满分12分)
-
11. 因式分解: .12. 如图,△ABC沿BC所在的直线平移到△DEF的位置,若∠ACF=85°,∠BED=120°,则∠EDF的度数为 .
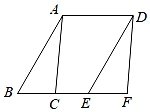 13. 某商场的一件商品标价为420元,进价为280元,商场准备打折销售,要使利润率不低于5%,最低打 折.14. 如图,四边形ABCD中,∠DAB=30°,连接AC,将△ABC绕点B逆时针旋转60°,点C的对应点与点D重合得到△EBD,若AB=5,AD=4,则AC的长度为 .
13. 某商场的一件商品标价为420元,进价为280元,商场准备打折销售,要使利润率不低于5%,最低打 折.14. 如图,四边形ABCD中,∠DAB=30°,连接AC,将△ABC绕点B逆时针旋转60°,点C的对应点与点D重合得到△EBD,若AB=5,AD=4,则AC的长度为 .
三、解答题(共11小题,计78分.解答应写出过程)
-
15. 因式分解:3m2n+18mn+27n.16. 如图,在△ABC中,利用尺规作AB边上的高CD.(不写作法,保留作图痕迹)
 17. 如图,在△ABC中.∠ABC=45°,AD⊥BC于点D,点E是AD上一点,且BE=AC,求证:∠1=∠C.
17. 如图,在△ABC中.∠ABC=45°,AD⊥BC于点D,点E是AD上一点,且BE=AC,求证:∠1=∠C.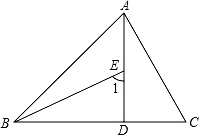 18. 如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8dm,r=1.6dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
18. 如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8dm,r=1.6dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π). 19. 解不等式组 ,并把不等式组的解集在数轴上表示出来.20. 如图,在三角形ABC中,DE是AC边的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=30°,求证:△ABD是等边三角形.
19. 解不等式组 ,并把不等式组的解集在数轴上表示出来.20. 如图,在三角形ABC中,DE是AC边的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=30°,求证:△ABD是等边三角形.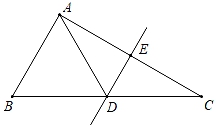 21. 如图,在Rt△ABC中,∠ACB=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
21. 如图,在Rt△ABC中,∠ACB=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.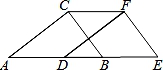 (1)、试求出∠E的度数;(2)、若AE=9cm,DB=2cm.请求出CF的长度.22. 如图,在平面直角坐标系中,已知△ABC各顶点的坐标分别为A(﹣5,2),B(﹣2,4),C(﹣1,1).
(1)、试求出∠E的度数;(2)、若AE=9cm,DB=2cm.请求出CF的长度.22. 如图,在平面直角坐标系中,已知△ABC各顶点的坐标分别为A(﹣5,2),B(﹣2,4),C(﹣1,1).
(1)平移△ABC,使点A平移到点A1的位置,画出平移后的△A1B1C1 , 并写出点C的对应点C1的坐标;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2 , 并写出点B的对应点B2的坐标.23. 某校购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且购买乙种树苗的棵数比甲种树苗棵数的2倍多30棵.(1)、若购买两种树苗的总费用不超过3400元,最多可以购买甲种树苗多少棵?(2)、为保证绿化效果,学校决定再购买甲、乙两种树苗共24棵(两种树苗都要买),总费用不超过500元,问有哪几种可能的购买方案?24. 如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.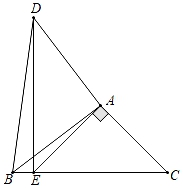 (1)、求证:DE⊥BC;(2)、若AC=3 ,BC=7,求线段BD的长.25. 疫情期间,“地摊经济”成为了社会关注的热门话题.小明从市场得知如下信息:
(1)、求证:DE⊥BC;(2)、若AC=3 ,BC=7,求线段BD的长.25. 疫情期间,“地摊经济”成为了社会关注的热门话题.小明从市场得知如下信息:甲商品
乙商品
进价(元/件)
35
5
售价(元/件)
45
8
小明计划购进甲、乙两种商品共100件进行销售.设小明购进甲商品x件,甲、乙商品全部销售完后获得的利润为y元.
(1)、求出y与x之间的函数关系式;(2)、小明用不超过2000元资金一次性购进甲,乙两种商品,最多可购进甲商品多少件?(3)、若购进乙商品的件数不少于甲商品件数的3倍,当购进甲,乙两种商品各多少件时,可使得甲、乙商品全部销售完后获得的利润最大?