江苏省镇江市句容市、丹徒区2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-08-03 类型：期中考试

进入 出卷网 下载

一、填空题（每小题2分，共24分）

  • 1. “日出东方”是事件.（填“确定”或“随机”）

    查看试题解析

  • 2. 在一个不透明的袋子中有1个红球，2个绿球和3个白球，这些球除了颜色外完全一样，摇匀后，从袋子中任意摸出1个球，你认为取出颜色的球的可能性最大.

    查看试题解析

  • 3. 在平行四边形ABCD中，∠A＝50°，则∠C＝ .

    查看试题解析

  • 4. 如图，△ABC绕点A按逆时针方向旋转50°后的图形为△AB1C1 ， 则∠ABB1＝ .

    查看试题解析

  • 5. 如图，矩形ABCD的对角线AC、BD相交于点O，∠ABO＝60°，若矩形的对角线长为2.则线段AD的长是 .

    查看试题解析

  • 6. 如图，菱形ABCD中，E，F分别是AD，BD的中点，若菱形ABCD的周长为20，则EF＝ .

    查看试题解析

  • 7. 如图，▱ABCD中AD＝2AB，CE平分∠BCD交AD边于点E，且AE＝4，则AB的长为 .

    查看试题解析

  • 8. 某班女生的体温测试被分成了三组，情况如表所示，则表中m的值是.

    第一组

    第二组

    第三组

    频数

    6

    8

    m

    频率

    p

    q

    30%

    查看试题解析

  • 9. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球，其中有a个白球和15个红球，若每次将球充分搅匀后，任意摸出1个球记下颜色后再放回盒子，通过大量重复试验后，发现摸到红球的频率稳定在0.3左右，则a的值约为 .

    查看试题解析

  • 10. 如图，连接四边形ABCD各边中点，得到四边形EFGH，只要添加条件，就能保证四边形EFGH是菱形．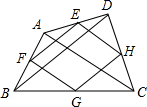

    查看试题解析

  • 11. 如图，直线a过正方形ABCD的顶点A，点B、D到直线a的距离分别为1、3，则正方形的边长为.

    查看试题解析

  • 12. 如图，将△ABC绕点A逆时针旋转45°得到△AB'C'，AB＝2，则图中阴影部分的面积为 .

    查看试题解析

二、选择（每小题3分，共21分）

  • 13. 下列垃圾分类的图标是中心对称图形的是（   ）.
    A、 厨余垃圾（绿色） B、 其他垃圾（黑色） C、 可回收物（蓝色） D、 有害垃圾（红色）

    查看试题解析

  • 14. 下列调查中，不适合采用全面调查方式的是（  ）
    A、了解新冠肺炎确诊病人同机乘客的健康情况 B、调查某中学在职教师的身体健康状况 C、对全校同学进行每日温度测量统计 D、中央电视台《开学第一课》的收视率

    查看试题解析

  • 15. 矩形具有而平行四边形不一定具有的性质是（    ）
    A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分

    查看试题解析

  • 16. 如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，把Rt△ABC绕着点A逆时针旋转，使点C落在AB边的C′上，C′B的长度是（ ）

    A、1 B、32 C、2 D、52

    查看试题解析

  • 17. 如图，▱ABCD中，对角线AC、BD相交于点O，OE⊥BD交AD于点E，连接BE，若▱ABCD的周长为18，则△ABE的周长为（  ）

    A、8 B、9 C、10 D、18

    查看试题解析

  • 18. 如图，在边长为1的正方形网格中，平行四边形ABCD的顶点在格点上，平行四边形EFGH的顶点E、F在边CD上，且AD∥EH，AD＝EH，AG交CD于点O，则S阴影为（  ）

    A、7平方单位 B、8平方单位 C、14平方单位 D、无法确定

    查看试题解析

  • 19. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，H是AF的中点，CH＝3，那么CE的长是（  ）

    A、3 B、4 C、15 D、17

    查看试题解析

三、解答题

  • 20. 已知：如图，在▱ABCD中，点E、F分别在BC、AD上，且BE＝DF

    求证：AC、EF互相平分.

    查看试题解析

  • 21. 某校为了解在春节期间学生在家的上网时间，随机抽查了该校若干名学生，对他们在春节期间的上网时间进行统计（每个学生只选一个选项），绘制了统计表和条形统计图.

    组别

    时间（小时）

    人数

    频数

    A

    0≤t＜1

    10

    0.1

    B

    1≤t＜2

    m

    0.2

    C

    2≤t＜3

    35

    0.35

    D

    3≤t＜4

    30

    n

    E

    4≤t＜5

    5

    0.05

    合计

    1

    根据以上信息回答下列问题：

    (1)、统计表中m＝ ， n＝.
    (2)、补全条形统计图；
    (3)、若该校有1230名学生，请估计该校学生春节期间在家上网时间少于2小时（不包含2小时）的人数.

    查看试题解析

  • 22. 在一个不透明的口袋里装有若干个相同的红球，为了用估计袋中红球的数量，八（1）班学生在数学实验室分组做摸球实验：每组先将10个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复．下表是这次活动统计汇总各小组数据后获得的全班数据统计表：

    摸球的次数s

    150

    300

    600

    900

    1200

    1500

    摸到白球的频数n

    63

    a

    247

    365

    484

    606

    摸到白球的频率 ns

    0.420

    0.410

    0.412

    0.406

    0.403

    b

    (1)、按表格数据格式，表中的a=；b=；
    (2)、请估计：当次数s很大时，摸到白球的频率将会接近（精确到0.1）；
    (3)、请推算：摸到红球的概率是（精确到0.1）；
    (4)、试估算：这一个不透明的口袋中红球有只．

    查看试题解析

  • 23. 如图，在△ABC中，O是AC上的任意一点（不与点A、C重合），过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.

    (1)、OE与OF相等吗？证明你的结论.
    (2)、试确定点O的位置，使四边形AECF是矩形，并加以证明.

    查看试题解析

  • 24. 如图，在△ABC中，AB＝AC，∠ABC＝50°. D是△ABC内任一点，将△ADC绕点A顺时针旋转，使点C与点B重合，点D的对应点为E.

    (1)、求证：EB＝DC；
    (2)、连接DE.

    ①若∠BED＝50°，则∠ADC＝ °；

    ②若E、D、C在一直线上，则∠BED＝时.

    查看试题解析

  • 25. 如图，正方形ABCD，E为平面内一点，且∠BEC＝90°，把△BCE绕点B逆时针旋转90°得△BAG，直线AG和直线CE交于点F.

    (1)、证明：四边形BEFG是正方形；
    (2)、若CE＝CF，则∠AGD＝°.

    查看试题解析

  • 26. 如图，将矩形纸片ABCD折叠，折叠后点B与点D重合，设折痕为EF，点E、F分别是折痕与AD、BC的交点.

    (1)、用直尺与圆规，作出折痕EF. （作图痕迹请用黑色笔描黑加粗）
    (2)、连接BE、DF，判断四边形EBFD的形状并说明理由.
    (3)、若AB＝4，BC＝8，则EF＝.

    查看试题解析

  • 27. 如图1所示，菱形ABCD的顶点A，B在x轴上，点A在点B的左侧，点D在y轴的正半轴上，其中点B（ 92 ，0）、D（0，6）.

    (1)、求C点的坐标；
    (2)、如图2，E是AD上一点，且AE＝ 114 ，P是AC上一动点，求PD+PE的最小值；
    (3)、如图3，动点Q从点B出发，以每秒 54 个单位长度的速度，沿折线B→C→D在菱形的两边上匀速运动，设运动时间为t秒.若点Q到BD的距离是 52 ，则t＝.

    查看试题解析