河南省郑州市2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2021-08-03 类型:期中考试
一、选择题(共10小题,每小题3分,共30分,每小题只有一个选项是符合题意的)
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将下列多项式分解因式,结果中不含因式x﹣1的是( )A、x2﹣1 B、x(x﹣2)+(2﹣x) C、x2﹣2x+1 D、x2+2x+13. 一元一次不等式组 的解集在数轴上表示正确的是( )A、
2. 将下列多项式分解因式,结果中不含因式x﹣1的是( )A、x2﹣1 B、x(x﹣2)+(2﹣x) C、x2﹣2x+1 D、x2+2x+13. 一元一次不等式组 的解集在数轴上表示正确的是( )A、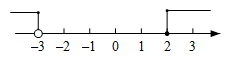
B、
B、 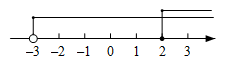
C、
C、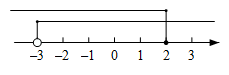
D、
D、
4. 若关于x的分式方程 ﹣ =0有增根,则a的值是( )A、a=﹣1 B、a=1 C、a=﹣2 D、a=25. 下列选项中,平行四边形不一定具有的性质是( )A、两组对边分别平行 B、两组对边分别相等 C、对角线互相平分 D、对角线相等6. 若分式 有意义且它的值为零,其中a、b、c为三角形的三条边,则此三角形一定为( )A、等腰三角形 B、等边三角形 C、各边都不相等的三角形 D、直角三角形7. 两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需x个月,则根据题意可列方程中错误的是( )A、 + =1 B、 + + =1 C、 + =1 D、 +2( + )=18. 如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
4. 若关于x的分式方程 ﹣ =0有增根,则a的值是( )A、a=﹣1 B、a=1 C、a=﹣2 D、a=25. 下列选项中,平行四边形不一定具有的性质是( )A、两组对边分别平行 B、两组对边分别相等 C、对角线互相平分 D、对角线相等6. 若分式 有意义且它的值为零,其中a、b、c为三角形的三条边,则此三角形一定为( )A、等腰三角形 B、等边三角形 C、各边都不相等的三角形 D、直角三角形7. 两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需x个月,则根据题意可列方程中错误的是( )A、 + =1 B、 + + =1 C、 + =1 D、 +2( + )=18. 如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )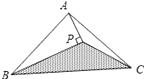 A、2cm2 B、3cm2 C、4cm2 D、5cm29. 如图,在平行四边形ABCD中,E是边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的度数为( )
A、2cm2 B、3cm2 C、4cm2 D、5cm29. 如图,在平行四边形ABCD中,E是边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的度数为( )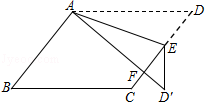 A、40° B、36° C、50° D、45°10. 如果关于x的分式方程 =1+ 有正整数解,且关于y的一元一次不等式组 的解集为y≤a,则所有满足条件的整数a的和为( )A、8 B、7 C、3 D、2
A、40° B、36° C、50° D、45°10. 如果关于x的分式方程 =1+ 有正整数解,且关于y的一元一次不等式组 的解集为y≤a,则所有满足条件的整数a的和为( )A、8 B、7 C、3 D、2二、填空题(共5小题,每小题3分,共15分)
-
11. 若 成立,则x的取值范围是.12. 已知a,b是一个等腰三角形的两边长,且满足a2+b2﹣6a﹣8b+25=0,则这个等腰三角形的周长为 .13. 如图,在Rt△ABC中,∠B=90°,∠BAC=30°,AC=6,将△ABC沿BC向右平移得到△DEF.若四边形ACFD的面积等于 ,则EC的长为.
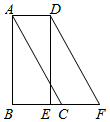 14. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,将△ABC绕点C逆时针旋转得到△A′B′C.且B′恰好落在AB上,连接AA′,取AA′的中点D,连接B′D,则B′D的为.
14. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,将△ABC绕点C逆时针旋转得到△A′B′C.且B′恰好落在AB上,连接AA′,取AA′的中点D,连接B′D,则B′D的为.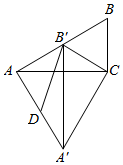 15. 如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连接AM、MN,若AC=6,AB=5,则AM﹣MN的最大值为.
15. 如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连接AM、MN,若AC=6,AB=5,则AM﹣MN的最大值为.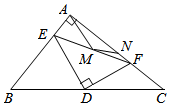
三、解答题(共7小题55分)
-
16.(1)、解分式方程: .(2)、化简求值:( +a﹣3)÷ ,a= ﹣1.17.
图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)
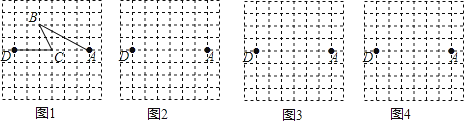 (1)、求1路车从A站到D站所走的路程(精确到0.1);(2)、在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)18. 已知:线段AB,BC.求作:平行四边形ABCD.以下是甲、乙两同学的作业.
(1)、求1路车从A站到D站所走的路程(精确到0.1);(2)、在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)18. 已知:线段AB,BC.求作:平行四边形ABCD.以下是甲、乙两同学的作业.甲:
①以点C为圆心,AB长为半径作弧;
②以点A为圆心,BC长为半径作弧;
③两弧在BC上方交于点D,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图1)
乙:
①连接AC,作线段AC的垂直平分线,交AC于点M;
②连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图2)
老师说甲、乙同学的作图都正确,你更喜欢__▲__的作法,他的作图依据是:_▲_.
 19. 对于任意两个数a、b的大小比较,有下面的方法:当a﹣b>0时,一定有a>b;当a﹣b=0时,一定有a=b;当a﹣b<0时,一定有a<b.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
19. 对于任意两个数a、b的大小比较,有下面的方法:当a﹣b>0时,一定有a>b;当a﹣b=0时,一定有a=b;当a﹣b<0时,一定有a<b.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
(1)、已知:A=2x2y+8y,B=8xy,且A>B,试判断y的符号;(2)、已知:a、b、c为三角形的三边,比较a2+c2﹣b2和2ac的大小.20. 春节期间,根据习俗每家每户都会在门口挂红灯笼和贴对联,某商店看准了商机,准备购进一批红灯笼和对联进行销售,已知每副对联的进价比每个红灯笼的进价少10元,且购进对联50幅比购进红灯笼20个多花费40元.(1)、对联和红灯笼的单价分别为多少?(2)、由于销售火爆,第一批售完后,该商店以相同的进价再购进300副对联和200个红灯笼,已知对联的销售价格为12元一幅,红灯笼的销售价格为24元一个,销售一段时间后发现对联售出了总数的 ,红灯笼售出了总数的 ,为了清仓,该店老板决定对剩下的红灯笼和对联以相同的折扣数打折销售,并很快全部售出,问商店最低打几折,才能使总的利润率不低于20%?21. 阅读下面材料,并解答问题.将分式 拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为x2﹣1,可设x4+x2﹣3=(x2﹣1)(x2+a)+b.
则x4+x2﹣3=(x2﹣1)(x2+a)+b=x4﹣x2+ax2﹣a+b=x4+(a﹣1)x2﹣a+b
∴ ,∴
∴ = = ﹣ =(x2+2)﹣
这样,分式 被拆分成了一个整式x2+2与一个分式﹣ 的和.
根据上述作法,将分式 拆分成一个整式与一个分式(分子为整数)的和的形式.
22. 如图1,在正方形ABCD中,点E,F分别在边AB,AD上,且AE=AF,延长FD到点G,使得DG=DF,连接EF,GE,CE.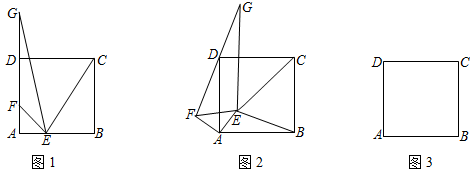 (1)、【特例感知】
(1)、【特例感知】图1中GE与CE的数量关系是.
(2)、【结论探索】如图2,将图1中的△AEF绕着点A逆时针旋转α(0°<α<90°),连接FD并延长到点G,使得DG=DF,连接GE,CE,BE,此时GE与CE还存在(1)中的数量关系吗?判断并说明理由.
(3)、【拓展应用】在(2)的条件下,若AB=5,AE=3 ,当△EFG是以EF为直角边的直角三角形时,请直接写出GE的长.