江苏省扬州市四校2021年数学中考二模联考试卷
试卷更新日期:2021-08-03 类型:中考模拟
一、单选题
-
1. 下列各数中,最大的数是( )A、 B、 C、0 D、12. 下列运算正确的是( )A、 B、 C、 D、3. 某次校运会共有13名同学报名参加百米赛跑,他们的预赛成绩各不相同,现取其中前6名参加决赛,小勇同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差4. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为 ,剩下的水量为 .下面能反映 与 之间的关系的大致图象是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图, ,则 _______度.( )
5. 如图, ,则 _______度.( ) A、70 B、150 C、90 D、1006. 如图,∠1的正切值为( )
A、70 B、150 C、90 D、1006. 如图,∠1的正切值为( )
 A、 B、 C、3 D、27. 将一个边长为4的正方形 分割成如图所示的9部分,其中 , , , 全等, , , , 也全等,中间小正方形 的面积与 面积相等,且 是以 为底的等腰三角形,则 的面积为( )
A、 B、 C、3 D、27. 将一个边长为4的正方形 分割成如图所示的9部分,其中 , , , 全等, , , , 也全等,中间小正方形 的面积与 面积相等,且 是以 为底的等腰三角形,则 的面积为( ) A、2 B、 C、 D、8. 在平面直角坐标系中,平行四边形ABCD的顶点A在y轴上,点C坐标为(﹣4,0),E为BC上靠近点C的三等分点,点B、E均在反比例函数y= (k<0,x<0)的图象上,若tan∠OAD= ,则k的值为( )
A、2 B、 C、 D、8. 在平面直角坐标系中,平行四边形ABCD的顶点A在y轴上,点C坐标为(﹣4,0),E为BC上靠近点C的三等分点,点B、E均在反比例函数y= (k<0,x<0)的图象上,若tan∠OAD= ,则k的值为( )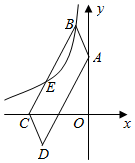 A、﹣2 B、﹣2 C、﹣6 D、﹣4
A、﹣2 B、﹣2 C、﹣6 D、﹣4二、填空题
-
9. 分解因式:6xy2﹣8x2y3=.10. 如果10m=12,10n=3,那么10m+n=.11. 若关于x的一元一次不等式组 的解集是x<﹣3,则m的取值范围是.12. 人的血管首尾相连的长度大约可达96000千米,96000千米用科学记数法表示为 米.13. 已知点 , 关于 轴对称,则 .14. 已知x﹣2y=1,则代数式3x﹣6y+2020的值是.15. 用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半轻是.16. 已知二次函数y=4x2﹣mx+5,当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,则当x=1时,y的值为.17. 如图,点E为正方形ABCD的边DA的延长线上一点,以BE为边在BE的另一侧作正方形BEFG,连接CG,若AB=12,BE=13,则△BCG的面积为.
 18. 如图,抛物线y= ﹣x﹣ 的图象与坐标轴交于A、B、D,顶点为E,以AB为直径画半圆交y轴的正半轴于点C,圆心为M,P是半圆AB上的一动点,连接EP,N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是.
18. 如图,抛物线y= ﹣x﹣ 的图象与坐标轴交于A、B、D,顶点为E,以AB为直径画半圆交y轴的正半轴于点C,圆心为M,P是半圆AB上的一动点,连接EP,N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是.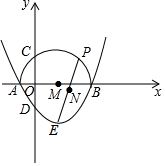
三、解答题
-
19.(1)、计算: .(2)、解方程: .20. 已知:BE⊥CD于E,BE=DE,BC=DA,
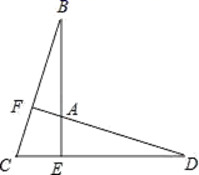 (1)、求证:△BEC≌△DEA;(2)、求证:BC⊥FD.21. 某厂生产A,B两种产品,其单价随市场变化而相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表:
(1)、求证:△BEC≌△DEA;(2)、求证:BC⊥FD.21. 某厂生产A,B两种产品,其单价随市场变化而相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表:第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:
=5.9;SA2= [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
(1)、求B产品三次单价的方差,并比较哪种产品的单价波动小;(2)、该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.22. 甲、乙、丙、丁四位同学参加校田径运动会4×100米接力跑比赛,因为丁的速度最快,所以由他负责跑最后一棒,其他三位同学的跑步顺序随机安排.(1)、请用画树状图或列表的方法表示甲、乙、丙三位同学所有的跑步顺序;(2)、请求出正好由丙将接力棒交给丁的概率.23. 有一段6000米的道路由甲、乙两个工程队负责完成,已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.(1)、求甲、乙两工程队每天各完成多少米?(2)、如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲、乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可合作施工多少天?(注:工作天数取整数)24. 如图将矩形ABCD沿CM折叠,使点D落在AB边上的点E处, (1)、求证:△AME∽△BEC.(2)、若△EMC∽△AME,求AB与BC的数量关系.25. 如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由 改为 .已知原传送带 长为 .
(1)、求证:△AME∽△BEC.(2)、若△EMC∽△AME,求AB与BC的数量关系.25. 如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由 改为 .已知原传送带 长为 . (1)、求新传送带 的长度;(2)、如果需要在货物着地点 的左侧留出 的通道,试判断距离 点 的货物 是否需要挪走,并说明理由.26. 已知:点D是△ABC的边AC上一点,tanC=1,cos∠ADB= ,⊙O经过B,C,D三点.
(1)、求新传送带 的长度;(2)、如果需要在货物着地点 的左侧留出 的通道,试判断距离 点 的货物 是否需要挪走,并说明理由.26. 已知:点D是△ABC的边AC上一点,tanC=1,cos∠ADB= ,⊙O经过B,C,D三点. (1)、若BD=4,求阴影部分图形的面积;(2)、若AD=2CD=4,求证:AB为⊙O的切线.27. 河上有一座桥孔为抛物线形的拱桥,水面宽为6米时,水面离桥孔顶部3米.把桥孔看成一个二次函数的图象,以桥孔的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图所示的平面直角坐标系.
(1)、若BD=4,求阴影部分图形的面积;(2)、若AD=2CD=4,求证:AB为⊙O的切线.27. 河上有一座桥孔为抛物线形的拱桥,水面宽为6米时,水面离桥孔顶部3米.把桥孔看成一个二次函数的图象,以桥孔的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图所示的平面直角坐标系. (1)、请求出这个二次函数的表达式;(2)、因降暴雨水位上升1米,此时水面宽为多少?28. 请认真阅读下列材料:
(1)、请求出这个二次函数的表达式;(2)、因降暴雨水位上升1米,此时水面宽为多少?28. 请认真阅读下列材料:如图①,给定一个以点O为圆心,r为半径的圆,设点A是不同于点O的任意一点,则点A的反演点定义为射线 上一点 ,满足 .
显然点A也是点 的反演点.即点A与点 互为反演点,点O为反演中心,r称为反演半径.这种从点A到点 的变换或从点 到点A的变换称为反演变换.

例如:如图②,在平面直角坐标系中,点 ,以点O为圆心, 为半径的圆,交y轴的正半轴于点B;C为线段 的中点,P是 上任意一点,点D的坐标为 ;若C关于 的反演点分别为 .
( 1 )求点 的坐标;
( 2 )连接 、 ,求 的最小值.
解:( 1 )由反演变换的定义知: ,其中 , .
∴ ,故点 的坐标为 ;
( 2 )如图③,连接 、 ,由反演变换知 ,
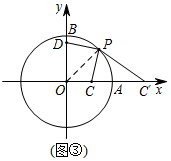
即 ,而 ,
∴ .
∴ ,即 .
∴ .
故 的最小值为13.
请根据上面的阅读材料,解决下列问题:
如图④,在平面直角坐标系中,点 ,以点O为圆心, 为半径画圆,交y轴的正半轴于点B,C为线段 的中点,P是 上任意一点,点D的坐标为 .

 (1)、点D关于 的反演点 的坐标为;(2)、连接 、 ,求 的最小值;(3)、如图⑤,以 为直径作 ,那么 上所有的点(点O除外)关于 的反演点组成的图形具有的特征是.
(1)、点D关于 的反演点 的坐标为;(2)、连接 、 ,求 的最小值;(3)、如图⑤,以 为直径作 ,那么 上所有的点(点O除外)关于 的反演点组成的图形具有的特征是.