江苏省苏州市2021年数学中考调研试卷(3月)
试卷更新日期:2021-08-03 类型:中考模拟
一、单选题
-
1. 下列四个数中,是负数的是( )A、 B、 C、 D、2. 下列四个图案中,不是中心对称图案的是( )A、
 B、
B、 C、
C、 D、
D、 3. 计算 的结果是( )A、 B、 C、 D、4. 某学习小组的五名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、74分,则下列结论正确的是( )A、平均分是91 B、中位数是90 C、众数是94 D、极差是205. 2018年某公司一月份的销售额是50万元,第一季度的销售总额为182万元,设第一季度的销售额平均每月的增长率为 ,可列方程为( )A、 B、 C、 D、6. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形7. 如图所示的飞镖游戏板是顺次连接正六边形的三个不相邻的顶点后得到的,若某人向该游戏板投掷镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( )
3. 计算 的结果是( )A、 B、 C、 D、4. 某学习小组的五名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、74分,则下列结论正确的是( )A、平均分是91 B、中位数是90 C、众数是94 D、极差是205. 2018年某公司一月份的销售额是50万元,第一季度的销售总额为182万元,设第一季度的销售额平均每月的增长率为 ,可列方程为( )A、 B、 C、 D、6. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形7. 如图所示的飞镖游戏板是顺次连接正六边形的三个不相邻的顶点后得到的,若某人向该游戏板投掷镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( ) A、1 B、 C、 D、8. 如图,点 在 上, , ,则 等于( )
A、1 B、 C、 D、8. 如图,点 在 上, , ,则 等于( )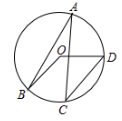 A、 B、 C、 D、9. 如图, ,点P在边 上, ,点M、N在边 上, ,若 ,则 是( )
A、 B、 C、 D、9. 如图, ,点P在边 上, ,点M、N在边 上, ,若 ,则 是( )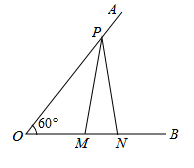 A、3 B、4 C、5 D、610. 如图,在平行四边形 中, , , ,点 、 分别是边 、 上的动点.连接 、 ,点 为 的中点,点 为 的中点,连接 .则 的最大值与最小值的差为( )
A、3 B、4 C、5 D、610. 如图,在平行四边形 中, , , ,点 、 分别是边 、 上的动点.连接 、 ,点 为 的中点,点 为 的中点,连接 .则 的最大值与最小值的差为( ) A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
11. 若二次根式 有意义,则x的取值范围是 .12. 分解因式:4a2-4a+1= .13. 已知圆锥的底面半径是 ,母线长为 ,则圆锥的侧面积为 .14. “五一”期间,某服装商店举行促销活动,全部商品八折销售,小华购买一件原价为140元的运动服,打折后他比按原价购买节省了元.15. 关于 的一元二次方程 有两个实数根,则 的取值范围是.16. 如图,一海轮位于灯塔 的西南方向,距离灯塔 海里的 处,它沿正东方向航行一段时间后,到达位于灯塔 的南偏东 方向上的 处,航程 的值为(结果保留根号).
 17. 已知关于x的二次函数y=ax2+2ax+a-3在-2≤x≤2时的函数值始终是负的,则常数a的取值范围是.18. 甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.给出下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有.(把你认为正确结论的序号都填上)
17. 已知关于x的二次函数y=ax2+2ax+a-3在-2≤x≤2时的函数值始终是负的,则常数a的取值范围是.18. 甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.给出下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有.(把你认为正确结论的序号都填上)
三、解答题
-
19. 计算: .20. 解不等式组 并在数轴上表示解集.21. 今年6月1日起苏州市全面实行垃圾分类,为了解同学们对垃圾分类知识的知晓情况,我区某校环保社团的同学们进行了抽样调查,对收集的信息进行整理,绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的数据,解答下列问题:

图中 表示“很了解”, 表示“了解”, 表示“一般”, 表示“不了解”.
(1)、被调查的总人数是人,扇形统计图中 部分所对应的扇形圆心角的度数为;(2)、若该校共有学生1800人,请根据上述调查结果,估计该校学生中 类有多少人.22. 如图,点B,F,C,E在一条直线上,AB=DE,∠B=∠E,BF=CE.求证:CG=FG.
 23. 某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
23. 某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)、求每个篮球和每个足球的售价;(2)、如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
24. 如图是某教室里日光灯的四个控制开关(分别记为A、B、C、D),每个开关分别控制一排日光灯(开关序号与日光灯的排数序号不一定一致).某天上课时,王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关.(1)、求王老师按下第一个开关恰好能打开第一排日光灯的概率;(2)、王老师按下两个开关恰好能打开第一排与第三排日光灯的概率是多少?请列表格或画树状图加以分析. 25. 如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
25. 如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、判断直线CD和⊙O的位置关系,并说明理由.(2)、过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.26.
(1)、判断直线CD和⊙O的位置关系,并说明理由.(2)、过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.26. (1)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明: 是 的黄金分割点;(2)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时, 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.(3)、我们知道:如图①,点 把线段 分成两部分,如果 ,那么称点 为线段 的黄金分割点.它们的比值为.(4)、在图①中,若 ,则 的长为 ;27. 如图,点 和动点 在直线 上,点 关于点 的对称点为 ,以 为边作 ,使 , ,作 的外接圆 .点 在点 右侧, ,过点 作直线 ,过点 作 于点 ,交 右侧的圆弧于点 .在射线 上取点 ,使 ,以 , 为邻边作矩形 .设 .
(1)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明: 是 的黄金分割点;(2)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时, 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.(3)、我们知道:如图①,点 把线段 分成两部分,如果 ,那么称点 为线段 的黄金分割点.它们的比值为.(4)、在图①中,若 ,则 的长为 ;27. 如图,点 和动点 在直线 上,点 关于点 的对称点为 ,以 为边作 ,使 , ,作 的外接圆 .点 在点 右侧, ,过点 作直线 ,过点 作 于点 ,交 右侧的圆弧于点 .在射线 上取点 ,使 ,以 , 为邻边作矩形 .设 . (1)、用关于 的代数式表示 , .(2)、当点 在点 右侧时,若矩形 的面积等于90,求 的长.(3)、当点 在点 右侧时,作直线 交 于点 ,若 的弦心距为1,求 的长.28. 如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y= x2﹣x交于A、B两点.
(1)、用关于 的代数式表示 , .(2)、当点 在点 右侧时,若矩形 的面积等于90,求 的长.(3)、当点 在点 右侧时,作直线 交 于点 ,若 的弦心距为1,求 的长.28. 如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y= x2﹣x交于A、B两点.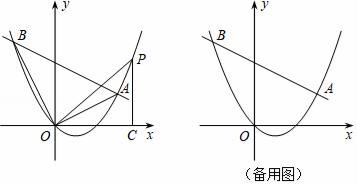 (1)、直线总经过定点,请直接写出该定点的坐标;(2)、点P在抛物线上,当k=﹣ 时,解决下列问题:
(1)、直线总经过定点,请直接写出该定点的坐标;(2)、点P在抛物线上,当k=﹣ 时,解决下列问题:①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.