江苏省南京市秦淮区2021年数学中考一模试卷
试卷更新日期：2021-08-03 类型：中考模拟
一、单选题
-
1. 已知a＜b，下列式子不成立的是（ ）A、a＋2021＜b＋2021 B、a－2021＜b－2021 C、－2021a＜－2021b D、 ＜2. 下列各数中，与 －1最接近的是（ ）A、0.4 B、0.6 C、0.8 D、13. 2020年是新中国历史上极不平凡的一年，我国经济运行逐季改善，在全球主要经济体中唯一实现经济正增长.根据国家统计局发布的数据，2016—2020年国内生产总值及其增长速度如图所示.
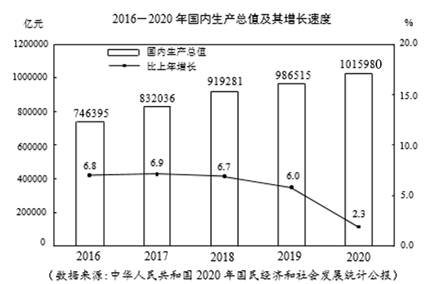
根据图中提供的信息，下列说法错误的是（ ）
A、 2020年末，中国的国内生产总值迈上百万亿元新的大台阶 B、2016年至2020年，国内生产总值呈递增趋势 C、2017年至2020年，相比较上一年，国内生产总值增加最多的是2017年 D、2017年至2020年，相比较上一年，国内生产总值增长速度最快的是2017年4. 关于一次函数y＝kx＋b，有下列命题：甲：图象过点（3，4）；乙：b＜0；丙：k＝2；丁：图象过点（1，2）.若上述四个命题中只有一个假命题，则该命题是（ ）A、甲 B、乙 C、丙 D、丁5. 将如图所示的纸片折叠、粘合成正方体形状.下列结论：
①粘合时，线段AB与线段FG重合；
②在正方体中，DE所在的面与GH所在的面相对；
③在正方体中，AC //DE；
④在正方体中，DE与EF的夹角是60°.
其中所有正确结论的序号是（ ）
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
6. 的相反数是 ， 的倒数是.7. “沉睡数千年，一醒惊天下”.三星堆遗址在5号坑提取出仅1.4 cm的牙雕制品，最细微处间隔不足50 μm（1μm＝10－6 m），用科学记数法表示50 μm是m.8. 分解因式： =.
9. 计算（a－b）2－（a＋b）2的结果是.10. 如图，在矩形ABCD中，AD＝6，AB＝4，∠BAD的平分线交BC于点E，则DE＝.
11. 如图，在△ABC中，D是AB上一点，∠ACD＝∠B，AC＝5，AD＝3，则DB＝.
12. 如图，AB是半圆的直径，C、D是半圆上的两点，且∠BAC＝46°， ＝ ，则∠DAB＝°.
13. 已知α、β是方程x2－2x－1＝0的两个根，则α2＋2β＝.14. 如图，在正方形ABCD中，E、F、G、H分别是DA、AB、BC、CD上靠近A、B、C、D的四等分点，I、J、K、L分别是EF、FG、GH、HE上靠近E、F、G、H的四等分点，则 ＝.
15. 如图，在四边形ABCD中，AB＝2，BC＝BD，∠ADC＝150°，∠DCB＝60°，则AC的最大值是.
三、解答题
-
16. 计算 .17. 解不等式组 并写出它的整数解.18. 如图，在菱形ABCD中，E、F是AC上两点，AE＝CF.
求证：四边形BFDE是菱形.
19. 某初中学校每天对全校学生的午休情况进行检查，初一，初二，初三3个年级都要被检查到.某天由甲，乙，丙3名同学检查，他们来自3个不同的年级，每人只能检查1个年级.(1)、甲检查初一年级的概率为；(2)、求他们都不检查自己所在年级的概率.20. 某初中学校共有2000名学生.为增强学生安全防护意识，该校提出“预防千万条，口罩第一条”的倡议——提倡在上学和放学途中佩戴口罩.学校数学兴趣小组采取简单随机抽样的方法，抽取了部分学生，了解其在上学和放学途中佩戴口罩的情况.(1)、收集数据
数学兴趣小组设计了以下三种调查方案：方案一：从初一年级随机抽取8个班级共300名学生进行调查；
方案二：分别从三个年级随机抽取各100名学生进行调查；
方案三：随机抽取300名女生进行调查.
其中抽取的样本具有代表性的方案是.
(2)、整理数据
数学兴趣小组采取（1）中的具有代表性的方案进行了一周的调查，根据调查，将数据绘制成如下的条形统计图：
估计全校周五上学途中佩戴口罩的学生人数是多少？(3)、比较这一周抽样学生上学、放学途中佩戴口罩的情况，写出一条正确的结论.21. “精准扶贫，暖心助力”.驻村书记通过某平台直播带货，帮助当地百姓脱贫致富.苹果成本价为每千克5元，销售价为每千克8元；蜜桔成本价为每千克6元，销售价为每千克10元.通过直播，两种水果共销售5000 kg，苹果的销售量不少于2000 kg.(1)、若销售的苹果和蜜桔的总成本为27400元，则销售苹果kg，销售蜜桔kg.(2)、当苹果的销量为多少时，两种水果的总利润最大？最大利润是多少？22. 如图，学校有一旗杆AB.为了测量旗杆高度，小明采用如下方案：在点C处测得旗杆顶B的仰角为45°，从与点C相距6 m的E处测得旗杆顶B的仰角为60°.若CD＝EF＝1.9 m，求旗杆AB的高度（精确到0.1 m）.（参考数据： ≈1.41， ≈1.73.）
23. 已知二次函数y=x2+2mx+m2-1（m为常数）.(1)、求证：不论m为何值，该函数的图象与x轴总有两个公共点；(2)、若函数的图象与x轴的两个公共点分别在原点的两侧，求m的取值范围.24. 如图，在Rt△ABC中，∠BAC＝90°，AB＝6，AC＝8.分别延长BA、AB、CA、AC至点D、E、F、G，使得AD＝AF＝BC，BE＝8，CG＝6.
(1)、经过D、E、G三点作⊙O；（尺规作图，保留作图痕迹，不写作法）(2)、求证：点F在⊙O上；(3)、⊙O的半径长为.25. （概念认识）已知m是实数，若某个函数图象上存在点M（m，m），则称点M是该函数图象上的“固定点”.
（数学理解）
(1)、一次函数y＝－2x＋3的图象上的“固定点”的坐标是；(2)、求证：反比例函数y＝ （k＞0）的图象上存在2个“固定点”；(3)、将二次函数y＝x2＋bx＋1（b＜－2）的图象在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分保持不变，翻折后的图象与原图象在x轴上方的部分组成一个类似“W”形状的新图象.若新图象上恰好存在3个“固定点”，求b的值.26. 如图①，已知∠MAN＝60°，点B在AM上，AB＝6，P是AN上一动点（点P不与点A重合），以AB、AP为相邻两边作平行四边形APCB，再以BP为直径作⊙O.
(1)、当 的某一边所在直线与⊙O相切时，AP的长为.(2)、当 的四条边所在直线与⊙O都相交时，设⊙O分别与AN、AM交于点E、G，与直线CP、BC交于点H、F.①如图②，在六边形BGEPHF中，易得BF//PE，BG //PH，∠GBF＝∠HPE＝120°，请再写出关于这个六边形的三个结论，并选择其中一个结论给出证明；
（要求：写出的三个结论类型不相同）
②设AP＝x，直接写出以B、G、E、P、H、F为顶点的六边形的面积（用含x的代数式表示）.