江苏省昆山市2021年九年级下学期数学联合调研测试（一）

试卷更新日期：2021-08-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、0 B、－1 C、 $\sqrt{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列运算结果正确的是（）

A、 $3 x - 2 x = 1$ B、 $x^{3} \div x^{2} = x$ C、 $x^{3} \cdot x^{2} = x^{6}$ D、 ${(x + y)}^{2} = x^{2} + y^{2}$

查看试题解析
3. 一个正常人的心跳平均每分70次，一天大约跳100800次，将100800用科学记数法表示为（　　）

A、0.1008×10⁶ B、1.008×10⁶ C、1.008×10⁵ D、10.08×10⁴

查看试题解析
4. 若 $a < - 1$ ，化简 $a + \sqrt{{(a + 1)}^{2}}$ 的结果等于（）

A、 $- 1$ B、 $1$ C、 $2 a - 1$ D、 $2 a + 1$

查看试题解析
5. 如图，△ABC中，AB＝AC，∠BAC、∠ABC的角平分线相交于点D.若∠ADB＝125°，则∠C等于（）

A、70° B、55° C、65° D、40°

查看试题解析
6. 如图，在四边形 $A B C D$ 中，已知 $A D / / B C$ ， $∠ B C D = 90 ° ， ∠ A B C = 45 ° ， B D$ 平分 $∠ A B C$ .若 $C D = 1$ cm，则 $A C$ 等于（）

A、 $\sqrt{2}$ cm B、 $\sqrt{3}$ cm C、2 cm D、3 cm

查看试题解析
7. 若二次函数y=x²＋bx的图象的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x²＋bx =5的解为（）

A、 $x_{1} = 0 ， x_{2} = 4$ B、 $x_{1} = 1 ， x_{2} = 5$ C、 $x_{1} = 1 ， x_{2} = - 5$ D、 $x_{1} = - 1 ， x_{2} = 5$

查看试题解析
8. 已知抛物线 $y = a x^{2} + b x + c$ $(b > a > 0)$ 与 $x$ 轴最多有一个交点，现有以下三个结论：①该抛物线的对称轴在 $y$ 轴右侧；②关于 $x$ 的方程 $a x^{2} + b x + c + 1 = 0$ 无实数根；③ $4 a + 2 b + c > 0$ ；其中，正确结论的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 如图，在等腰 $Δ A B C$ 中， $A B = A C ， B C = 3 \sqrt{10} ， \sin A = \frac{3}{5}$ ，则 $A B$ 的长为（）

A、15 B、 $5 \sqrt{10}$ C、20 D、 $10 \sqrt{5}$

查看试题解析
10. 如图，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过 $▱ O A B C$ 的顶点 $C$ 和对角线的交点 $E$ ，顶点 $A$ 在 $x$ 轴上.若 $▱ O A B C$ 的面积为12，则 $k$ 的值为（）

A、8 B、6 C、4 D、2

查看试题解析

二、填空题

11. 若代数式 $\frac{\sqrt{x}}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 分解因式： $a^{3} - 4 a$ ＝.

查看试题解析
13. 已知 $x - 2 y = 5$ ，那么代数式 $3 - 2 x + 4 y$ 的值是.

查看试题解析
14. 分式方程 $\frac{x}{x - 1} + 1 = \frac{3}{1 - x}$ 的解是.

查看试题解析
15. 如图， $Δ A B O$ 中， $A B ⊥ O B$ ， $O B = \sqrt{3}$ ， $A B = 1$ ，把 $Δ A B O$ 绕点 $O$ 顺时针旋转150°后得到 $Δ A_{1} B_{1} O$ ，则点 $B_{1}$ 的坐标为.

查看试题解析
16. 已知点P的坐标为（m， $m^{2} - 2 m - 3$ ），则点P到直线y＝﹣5的最小值为.

查看试题解析
17. 如图，已知l₁∥l₂∥l₃ ，相邻两条平行直线间的距离相等，若等腰直角三角形ABC的直角顶点C在l₁上，另两个顶点A，B分别在l₃ ， l₂上，则sinα的值是.

查看试题解析
18. 如图，矩形 $A B C D$ 中AB＝2，AD＝5，动点P从点A出发，以1 cm/s的速度沿AD向终点D移动，设移动时间为t（s）.连接PC，以PC为一边作正方形PCEF，连接DE、DF，则 $Δ D E F$ 面积最小值为.

查看试题解析

三、解答题

19. 计算： $| \sqrt{3} - 1 | + {(- 1)}^{2020} - \tan 60 °$

查看试题解析
20. 先化简，再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} + 2 x + 1}{x + 2}$ ，其中 $x = \sqrt{3} - 1$ .

查看试题解析
21. 解不等式组： ${\begin{cases} x + 1 \geq 2 \\ 3 (x - 1) > x + 5 \end{cases}$

查看试题解析
22. 我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球，一共需要花费2050元；如果购买10个甲种规格的排球和20个乙种规格的足球，一共需要花费1900元.

(1)、求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?

(2)、如果学校要购买甲种规格的排球和乙种规格的足球共50个，并且预算总费用不超过3210元，那么该学校至多能购买多少个乙种规格的足球?

查看试题解析
23.
如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．

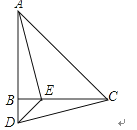(1)、求证：△ABE≌△CBD；

(2)、若∠CAE=30°，求∠BDC的度数．

查看试题解析
24. 如图，一艘渔船位于码头M的南偏东45°方向，距离码头120海里的B处，渔船从B处沿正北方向航行一段距离后，到达位于码头北偏东60°方向的A处．

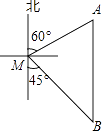(1)、求渔船从B到A的航行过程中与码头M之间的最小距离．

(2)、若渔船以20海里/小时的速度从A沿AM方向行驶，求渔船从A到达码头M的航行时间．

查看试题解析
25. 关于x的一元二次方程 $x^{2} - (2 m + 1) x + m = 0$ .

(1)、求证：方程总有两个不相等的实数根；

(2)、若 $x_{1}$ ， $x_{2}$ 是该方程的两根，且满足两根的平方和等于3，求m的值.

查看试题解析
26. 如图，在平面直角坐标系中，已知△ABC，∠ABC=90°，顶点A在第一象限，B、C在x轴的正半轴上（C在B的右侧），BC=3，AB=4，若双曲线 $y = \frac{k}{x} (k \neq 0)$ 交边AB于点E，交边AC于中点D.

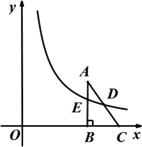(1)、若OB=2，求k；

(2)、若AE= $\frac{3}{8} A B$ ，求直线AC的解析式.

查看试题解析
27. 如图，抛物线y= $- \frac{1}{4}$ x²+bx+c与x轴交于点A（2，0），交y轴于点B（0， $\frac{5}{2}$ ）．直线y=kx $- \frac{3}{2}$ 过点A与y轴交于点C，与抛物线的另一个交点是D．

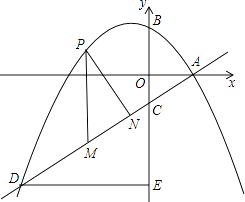(1)、求抛物线y= $- \frac{1}{4}$ x²+bx+c与直线y=kx $- \frac{3}{2}$ 的解析式；

(2)、设点P是直线AD上方的抛物线上一动点（不与点A、D重合），过点P作y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；

(3)、在（2）的条件下，作PN⊥AD于点N，设△PMN的周长为l，点P的横坐标为x，求l与x的函数关系式，并求出l的最大值．

查看试题解析