湖北省枣阳市2021年数学中考适应性试卷
试卷更新日期:2021-08-03 类型:中考模拟
一、单选题
-
1. 如果把收入100元记作+100元,那么支出80元记作( )A、+20元 B、+100元 C、+80元 D、-80元2. 下列运算正确的是( )A、2a+3a=5a2 B、(﹣ab2)3=﹣a3b6 C、a2•a3=a6 D、(a+2b)2=a2+4b23. 如图,已知直线AB∥CD,直线AC和BD相交于点E,若∠ABE=75°,∠ACD=35°,则∠AEB等于( )
 A、60° B、70° C、75° D、80°4. 下列几何体中,主视图是长方形的是( )A、
A、60° B、70° C、75° D、80°4. 下列几何体中,主视图是长方形的是( )A、 B、
B、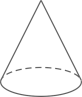 C、
C、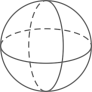 D、
D、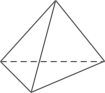 5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 不等式组 的解集是( ).A、 B、 C、 D、7. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=144°,则∠C的度数是( )
6. 不等式组 的解集是( ).A、 B、 C、 D、7. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=144°,则∠C的度数是( ) A、108° B、106° C、104° D、102°8. 两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )A、两个小球的标号之和等于1 B、两个小球的标号之和等于6 C、两个小球的标号之和大于1 D、两个小球的标号之和大于69. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、10. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+ac的 图象不经过( )
A、108° B、106° C、104° D、102°8. 两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )A、两个小球的标号之和等于1 B、两个小球的标号之和等于6 C、两个小球的标号之和大于1 D、两个小球的标号之和大于69. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、10. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+ac的 图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
11. 今年清明节期间,襄阳市旅游市场持续火爆,全市共接待境内外游客超过287000人次,请将287000用科学记数法表示为.12. 为把我市创建成全国文明城市,某社区积极响应市政府号召,准备在 一块正方形的空地上划出部分区域栽种鲜花,如图中的阴影“┛”带,鲜花带一边宽1m.另一边宽2m,剩余空地的面积为18m2 , 求原正方形空地的边长 m,可列方程为.
 13. 如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: .
13. 如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: . 14. 已知电流在一定时间段内正常通过电子元件“
14. 已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5,则在一定时间段内,由该元件组成的图示电路 , 之间,电流能够正常通过的概率是.
”的概率是0.5,则在一定时间段内,由该元件组成的图示电路 , 之间,电流能够正常通过的概率是.  15. 竖直上抛物体时,物休离地而的高度 与运运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时高地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为m.16. 如图,已知矩形ABCD中,AB=3,BC=4,点M,N分别在边AD,BC上,沿着MN折叠矩形ABCD,使点A,B分别落在E,F处,且点F在线段CD上(不与两端点重合),若 ,则折叠后重叠部分的面积为.
15. 竖直上抛物体时,物休离地而的高度 与运运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时高地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为m.16. 如图,已知矩形ABCD中,AB=3,BC=4,点M,N分别在边AD,BC上,沿着MN折叠矩形ABCD,使点A,B分别落在E,F处,且点F在线段CD上(不与两端点重合),若 ,则折叠后重叠部分的面积为.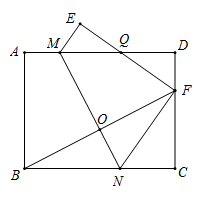
三、解答题
-
17. 先化简,再求值: ,其中 .18. 某校为了解九年级学生课外阅读古典名著情况,特对他们的每周课外阅读名著时长(单位:小时)进行统计.现随机抽取20名学生的数据进行分析:
收集数据:
4.5,6,5.5,6.5,6.5,5.5,7,6,7.5,8,6.5,8,7.5,5.5,6.5,7,6.5,6,6.5,5
整理数据:
时长 (小时)
4< ≤5
5< ≤6
6< ≤7
7< ≤8
人数
2
8
4
分析数据:
项目
平均数
中位数
众数
数据
6.4
应用数据:
(1)、填空:a= , b=; = ;补全频数分布直方图; (2)、这组数据用扇形统计图表示,时长在6< ≤7范围内的扇形圆心角的大小为度;(3)、若九年级共有1000人,请估计课外阅读名著时长.在5<x≤7小时的人数约为人.19. 如图,正方形ABCD中,G是BC边上任意一点(不与B、C重合),DE⊥AG于点E, BF⊥AG于F.
(2)、这组数据用扇形统计图表示,时长在6< ≤7范围内的扇形圆心角的大小为度;(3)、若九年级共有1000人,请估计课外阅读名著时长.在5<x≤7小时的人数约为人.19. 如图,正方形ABCD中,G是BC边上任意一点(不与B、C重合),DE⊥AG于点E, BF⊥AG于F. (1)、在图中用直尺和圆规作BF⊥AG于F,保留作图痕迹,不写作法;(2)、求证:AF-BF=EF.20. 某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,(结果精确到0.lm.温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27)
(1)、在图中用直尺和圆规作BF⊥AG于F,保留作图痕迹,不写作法;(2)、求证:AF-BF=EF.20. 某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,(结果精确到0.lm.温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27) 21. 参照学习函数的过程与方法,探究函数 ( ≠0)的图象与性质.因为 ,即 ,所以我们对比函数 来探究.
21. 参照学习函数的过程与方法,探究函数 ( ≠0)的图象与性质.因为 ,即 ,所以我们对比函数 来探究.列表:
…
-4
-3
-2
-1
1
2
3
4
…
…
1
2
4
-4
-2
-1
…
…
2
5
-3
-1
0
…
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点,如图所示.
 (1)、表中的 ;(2)、请把 轴左边各点和右边各点分别用一条光滑曲线顺次连接起来;(3)、观察图象并分析表格,回答下列问题:
(1)、表中的 ;(2)、请把 轴左边各点和右边各点分别用一条光滑曲线顺次连接起来;(3)、观察图象并分析表格,回答下列问题:①当 <0时, 随 的增大而 ▲ ;(填“增大”或“减小”)
② 的图象是由 的图象向 ▲ 平移 ▲ 个单位得到的;
③图象关于点 ▲ 中心对称;(填点的坐标);
④图象是轴对称图形,对称轴是 ▲ .(填解析式)
22. 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD cm. (1)、求证:AC是⊙O的切线;(2)、求图中阴影部分的面积(结果保留 ).23. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出 型和 型两款垃圾分拣机器人,已知 台 型机器人和 台 型机器人同时工作 共分拣垃圾 吨, 台 型机器人和 台 型机器人同时工作 共分拣垃圾 吨.(1)、1台 型机器人和 台 型机器人每小时各分拣垃圾多少吨?(2)、某垃圾处理厂计划向机器人公司购进一批 型和 型垃圾分拣机器人,这批机器人每小时一共能分拣垃圾 吨.设购买 型机器人 台 , 型机器人 台,请用含 的代数式表示 ;(3)、机器人公司的报价如下表:
(1)、求证:AC是⊙O的切线;(2)、求图中阴影部分的面积(结果保留 ).23. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出 型和 型两款垃圾分拣机器人,已知 台 型机器人和 台 型机器人同时工作 共分拣垃圾 吨, 台 型机器人和 台 型机器人同时工作 共分拣垃圾 吨.(1)、1台 型机器人和 台 型机器人每小时各分拣垃圾多少吨?(2)、某垃圾处理厂计划向机器人公司购进一批 型和 型垃圾分拣机器人,这批机器人每小时一共能分拣垃圾 吨.设购买 型机器人 台 , 型机器人 台,请用含 的代数式表示 ;(3)、机器人公司的报价如下表:型号
原价
购买数量少于 台
购买数量不少于 台
型
万元/台
原价购买
打九折
型
万元/台
原价购买
打八折
在 的条件下,设购买总费用为 万元,问如何购买使得总费用 最少?请说明理由.
24. (1)、类比延伸
(1)、类比延伸如图2,在Rt△ABC和Rt△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE=30°,连接BD,CE,试确定BD与CE的数量关系,并说明理由.
(2)、拓展迁移如图3,在四边形ABCD中,AC⊥BC,且AC=BC,CD=4,若将线段DA绕点D按逆时针方向旋转90°得到DA′,连接BA′,求线段BA′的长.
(3)、问题探究:如图1,△ABC,△ADE均为等边三角形,连接BD、CE,试探究线段BD与CE的数量关系,并说明理由.
25. 如图,函数 的图象经过点A(m,0),B(0,n)两点,与x轴的另一个交点为C,m,n分别是方程 的两个实数根,且m<n.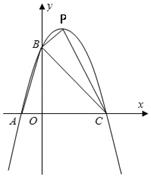 (1)、求m,n的值以及函数的解析式;(2)、设P是抛物线 第一象限上一动点,连接PB,PC,当△PBC的面积最大时,求点P的坐标,并求出最大面积;(3)、对于函数 ,设函数 在 ≤ ≤ +1内的最大值为p,最小值为q,若p﹣q=3,求t的值.
(1)、求m,n的值以及函数的解析式;(2)、设P是抛物线 第一象限上一动点,连接PB,PC,当△PBC的面积最大时,求点P的坐标,并求出最大面积;(3)、对于函数 ,设函数 在 ≤ ≤ +1内的最大值为p,最小值为q,若p﹣q=3,求t的值.