湖北省襄阳市南漳县2021年数学中考适应性考试试卷

试卷更新日期：2021-08-03 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{1}{2021}$ 的相反数是（）

A、 $\frac{1}{2021}$ B、 $- \frac{1}{2021}$ C、 $2021$ D、 $- 2021$

查看试题解析
2. 下列运算结果正确的是（）

A、a⁶÷a³＝a² B、（a²）³＝a⁵ C、3a＋2a＝5a² D、a²－（－a）²＝0

查看试题解析
3. 下列四个几何体中，左视图与俯视图相同的是（）

A、 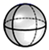B、 C、 D、

查看试题解析
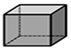4. 不等式组 ${\begin{array}{l} 2 x + 3 \geq 1 \\ x - 2 < 0 \end{array}$ 的解集在数轴上可表示为（）

A、 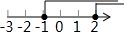B、 C、 D、

查看试题解析
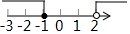5. 如图，AB $//$ CD，AD⊥AC，∠BAD＝35°，则∠ACD＝（）

A、35° B、45° C、55° D、70°

查看试题解析
6. 参加一次绿色有机农产品交易会的每两家公司都签订了一份合同，所有公司共签订了45份合同，参加这次交易会的公司共有（）

A、9家 B、10家 C、10家或9家 D、19家

查看试题解析
7. 如图，已知菱形ABCD的边长为2，∠DAB=60°，则对角线BD的长是（）

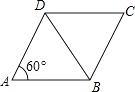A、1 B、 $\sqrt{3}$ C、2 D、2 $\sqrt{3}$

查看试题解析
8. 下列事件中，属于必然事件的是（）

A、如果x²＝y² ，那么x＝y B、车辆行驶到某十字路口，遇到绿灯 C、掷一枚1元的硬币，有数字的面向上 D、太阳每天都会从东方升起

查看试题解析
9. 如图，AB是⊙O的直径，⊙O的弦CD＝8，且CD⊥AB于点E. 若OE∶OB＝3∶5，则直径AB的长为（）

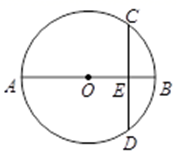A、16 B、13 C、10 D、6

查看试题解析
10. 下列叙述正确的是（）

A、 $\sqrt{4}$ 的算术平方根是2 B、函数y＝ $\sqrt{x + 1}$ 的自变量x的取值范围是x＞－1 C、一元二次方程x²－2x＝4无实数根 D、若点P（m，－1）与点Q（5，n）关于坐标原点对称，则m＝－5，n＝1

查看试题解析

二、填空题

11. 被命名为COVID-19新型冠状病毒的平均直径约是0.00 000 009米，将0.00 000 009用科学记数法表示为.

查看试题解析
12. 某校举行以“学党史，感党恩，听党话，跟党走”为主题的演讲比赛，决赛阶段只剩下甲、乙、丙、丁四名同学，则甲、乙同学获得前两名的概率是.

查看试题解析
13. 《九章算术》是中国古代一部数学专著，其中有一道阐述“盈不足术”的问题.原文：今有人共买物，人出八，盈三；人出七，不足四.问人数，物价各几何？译文：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元. 问共有多少人？这个物品的价格是元.

查看试题解析
14. 某种商品每件进价为20元，调查表明：在某段时间内，若以每件x元（20≤x≤40，且x为整数）出售，可卖出（40﹣x）件，若要使利润最大，则每件商品的售价应为元.

查看试题解析
15. 如图，△ABC内接于⊙O， E是边BC的中点，连接OE并延长交⊙O于点D，连接CD，若∠BCD＝26°，则∠A＝°.

查看试题解析
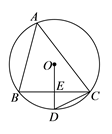16. 如图，矩形ABCD中，AB＝5，BC＝3，E为边AB上一点，且BE＝3，△DAE沿DE翻折得到△DFE，连接BF，tan∠EFB的值为.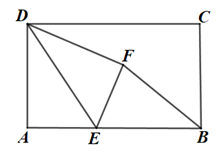

查看试题解析

三、解答题

17. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{x - 1} \div (\frac{3}{x - 1} - x - 1)$ ，其中x＝ $\sqrt{2}$ －2.

查看试题解析
18. 如图，△ABC中，AB＝AC，AD是边BC上的高.

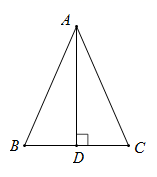(1)、请用尺规作图法，作出线段AD的垂直平分线MN（保留作图痕迹，不必写出作法，但必须交待作图结果）；

(2)、设（1）中的直线MN交边AB，AC分别于点E，F ，连接DE，DF.求证：四边形AEDF是菱形.

查看试题解析
19. 为了解学生掌握垃圾分类知识的情况，某校举行有关垃圾分类的知识测试活动，现从七、八年级中各随机抽取20名学生的测试成绩（满分10分，6分及6分以上为合格）进行整理、描述和分析，下面给出了部分信息.
七年级20名学生的测试成绩为：

7，8，7，9，7，6，5，9，10，9，8，5，8，7，6，7，9，7，10，6.

八年级20名学生的测试成绩条形统计图如图所示：

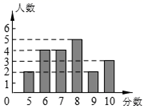
七，八年级抽取的学生的测试成绩的平均数、众数、中位数如表所示：

年级

平均数

众数

中位数

七年级

7.5

b

7

八年级

a

8

c

请你根据以上提供信息，解答下列问题：

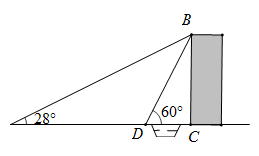
(1)、上表中a＝， b＝， c＝；

(2)、根据以上数据，你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好？请说明理由（写出一条理由即可）；

(3)、该校七、八年级共1100名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生有人.

查看试题解析
20. 如图，某中学数学兴趣小组在学习了“解直角三角形及其应用”后，选定测量小河对岸一幢建筑物BC的高度，他们先在A处测得该建筑物顶端B的仰角为28°，然后从A处前进40m到达D处，在D处测得该建筑物顶端B的仰角为60°，点A，D， C在同一水平的直线上，且BC⊥DC. 求建筑物BC的高度（结果精确到0.1）.
（参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53， $\sqrt{3}$ ≈1.73）

查看试题解析

21. 张明丽同学学习了反比例函数 y＝－

\frac{6}{x}

的图象和性质后，对新函数y＝－

\frac{6}{x - 2}

的图象和性质进行了探究，以下是她的探究过程：

第一步：在平面直角坐标系中，作出函数 y＝－ $\frac{6}{x}$ 的图象；

第二步：通过列表、描点、连线，作出新函数y＝－ $\frac{6}{x - 2}$ 的图象；

①列表：

x	…	－4	－2	－1	0	1	3	4	5	6	…
y	…	1	$\frac{3}{2}$	2	3	6	－6	－3	－2	－ $\frac{3}{2}$	…

②描点：如图所示

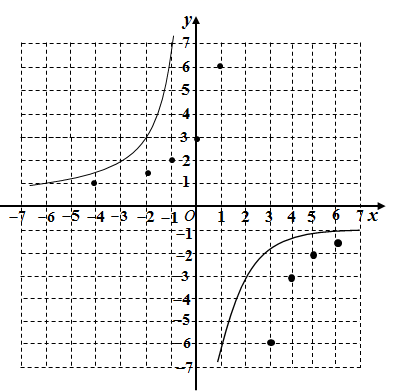(1)、请在图中帮助张明丽同学完成连线步骤；

(2)、观察函数图象，发现函数y＝－

\frac{6}{x - 2}

与函数 y＝－

\frac{6}{x}

的图象都是双曲线，并且形状也相同，只是位置发生了改变，由此可知，函数y＝－

\frac{6}{x - 2}

的图象可由函数 y＝－

\frac{6}{x}

的图象平移得到.请结合图象写出函数y＝－

\frac{6}{x - 2}

的两条性质（函数的增减性和对称性各一条）.

查看试题解析

22. 如图，在等腰△ABC中，AB＝BC，以AB为直径的⊙O与AC相交于点D，与CB的延长线相交于点E，过点D作DF⊥BC交AB的延长于点F，垂足为点M.

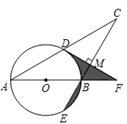(1)、判定直线DF与⊙O的位置关系，并说明理由；

(2)、若BF＝4，∠F＝30°，求图中阴影部分的面积.

查看试题解析
23. 某校计划对100名获优秀作品一、二、三等奖的学生分别奖励一套数学用具、一本笔记本、一支水笔. 已知购买1套数学用具和2本笔记本共35元，购买2套数学用具和3本笔记本共60元，一支水笔的单价为2元. 已知获一等奖人数最少，获三等奖的人数最多.

(1)、求数学用具和笔记本的单价；

(2)、因购买数量较多，商家给予优惠：每买1套数学用具和1本笔记本赠送2支水笔；
①若获二等奖人数是获一等奖人数的1.5倍，且获一等奖人数超过20人，已知在购买奖品时仍需要购买水笔，求购买奖品的总金额；

②若赠送的水笔恰好奖励给获三等奖的学生，求购买奖品的总金额的最小值及获二等奖的人数.

查看试题解析
24. 在△ABC中，AB＝AC，∠BAC＝α，点P是△ABC外一点，连接BP，将线段BP绕点P逆时针旋转α得到线段PD，连接BD，CD，AP.
观察猜想：

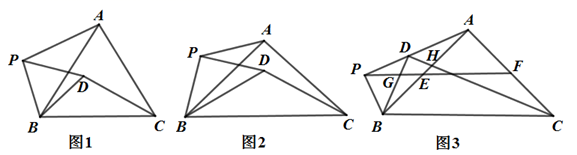(1)、如图1，当α＝60°时， $\frac{C D}{A P}$ 的值为，直线CD与 AP所成的较小角的度数为°；
类比探究：

(2)、如图2，当α＝90°时，求出 $\frac{C D}{A P}$ 的值及直线CD与AP所成的较小角的度数；

(3)、如图3，当α＝90°时，点E，F分别为AB，AC的中点，点P在线段FE的延长线上，点A，D，P三点在一条直线上，BD交PF于点G，CD交AB于点H. 若CD＝2＋ $\sqrt{2}$ ，求BD的长.

查看试题解析
25. 在平面直角坐标系xOy中，矩形OABC的顶点A，C的坐标分别为（0，3），（2，0），顶点为M的抛物线y＝－x²＋bx＋c经过点A，B，且与x轴交于点D，E（点D在点E的左侧）.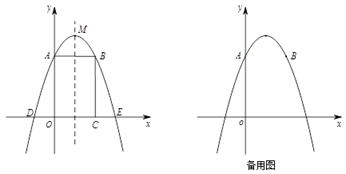

(1)、直接写出点B的坐标，抛物线的解析式及顶点M的坐标；

(2)、点P是（1）中抛物线对称轴上一动点，求△PAD的周长最小时点P的坐标；

(3)、平移抛物线y＝－x²＋bx＋c，使抛物线的顶点始终在直线AM上移动，在平移的过程中，当抛物线与线段BM有公共点时，求抛物线顶点的横坐标a的取值范围.

查看试题解析

年级	平均数	众数	中位数
七年级	7.5	b	7
八年级	a	8	c