湖北省老河口市2021年数学中考适应性考试试卷
试卷更新日期:2021-08-03 类型:中考模拟
一、单选题
-
1. 下列各数中,绝对值最大的数是( )
A、-3 B、-2 C、0 D、2 -
2. 下列各式计算结果是a6的是( )A、a3+a3 B、a12÷a2 C、a2•a3 D、(﹣a3)2
-
3. 如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
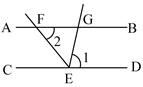 A、20° B、40° C、50° D、60°
A、20° B、40° C、50° D、60° -
4. 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )
 A、① B、② C、③ D、④
A、① B、② C、③ D、④ -
5. 不等式组 的解集,在数轴上表示正确的是( )A、
 B、
B、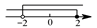 C、
C、 D、
D、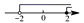
-
6. 下列说法正确的是( )A、“购买一张彩票,中奖”是不可能事件 B、“从 , ,π,0.2这四个数中随机选一个数,这个数是无理数”是随机事件 C、抛掷一枚质地均匀的硬币10次,有3次正面朝上,说明正面朝上的概率是0.3 D、某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是0.5
-
7. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、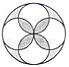 C、
C、 D、
D、
-
8. 分式方程 的解是( )A、x=1 B、x=﹣1+ C、x=2 D、无解
-
9. 如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
 A、四边形AEDF是平行四边形 B、若∠BAC=90°,则四边形AEDF是矩形 C、若AD平分∠BAC,则四边形AEDF是矩形 D、若AD⊥BC且AB=AC,则四边形AEDF是菱形
A、四边形AEDF是平行四边形 B、若∠BAC=90°,则四边形AEDF是矩形 C、若AD平分∠BAC,则四边形AEDF是矩形 D、若AD⊥BC且AB=AC,则四边形AEDF是菱形 -
10. 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
 A、
A、 B、
B、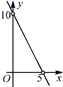 C、
C、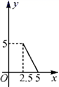 D、
D、
二、填空题
-
11. 截止2021年4月中国高速路总里程达16万公里.请将“16万”用科学记数法表示记为.
-
12. 某种服装原价每件80元,经两次降价,现售价每件64.8元,这种服装平均每次降价的百分率是.
-
13. 从A,B,C,D四名同学中,随机抽取三人代表某学校参加文艺表演,抽到A,B,C三人的概率是.
-
14. 用长为12米的铝合金条制成如图所示的窗框,若窗框的高为x米,当x等于时窗户的透光面积最大(铝合金条的宽度不计).

-
15. PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为.
-
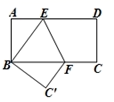
16. 如图,在矩形ABCD中,点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠使点D与点B重合,点C的对应点是点C'.若AB=4,EF= ,则AD的长等于.
三、解答题
-
17. 先化简,再求值 ,其中 , .
-
18. 某校为了了解A,B两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对成绩进行整理、描述和分析,下面给出了部分信息.
①A,B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
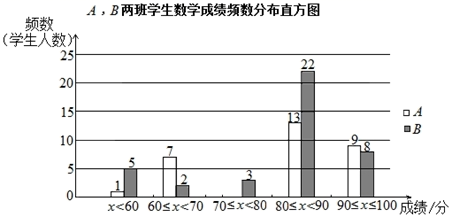
②A,B两班学生测试成绩在80≤x<90这一组的数据如下︰
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
A,B两班学生测试成绩的平均数、中位数、方差如下:
平均数
中位数
方差
A班
80.6
m
96.9
B班
80.8
n
153.3
根据以上信息,回答问题:
(1)、A班有人,其中成绩在70≤x<80这一组的有人;(2)、表中m= , n=;(3)、从两个方面来分析A,B两班的成绩:① ▲ ,② ▲ . -
19. 如图,AE∥BF,AC平分∠BAE,且交BF于点C.
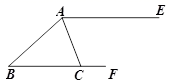 (1)、作∠ABF的平分线交AE于点D(尺规作图,保留痕迹,不写作法);(2)、根据(1)中作图,连接CD,求证:四边形ABCD是菱形.
(1)、作∠ABF的平分线交AE于点D(尺规作图,保留痕迹,不写作法);(2)、根据(1)中作图,连接CD,求证:四边形ABCD是菱形. -
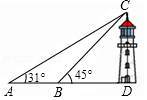
20. 如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行30m到达B处,测得该灯塔的最高点C的仰角为45°,根据测得的数据,计算这座灯塔的高度CD(结果取整数).
参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.
-
21. 小明在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其探究过程如下:(1)、绘制函数图象,如图,
列表:下表是x与y的几组对应值,其中 = ▲ ;
x
…
-3
-2
-1
1
2
3
…
y
…
-1
-2
m
-1
…
描点:根据表中各组对应值( , ),在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象,请你把图象补充完整;
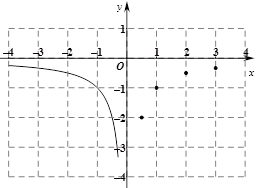 (2)、通过观察图象,写出该函数的两条性质:① ▲ ;② ▲ .
(2)、通过观察图象,写出该函数的两条性质:① ▲ ;② ▲ . -
22. 如图,AB是⊙O的直径,OC⊥AD,CE⊥AB于点E,AC平分∠PAD.
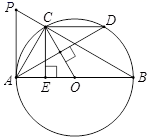 (1)、求证:PA是⊙O的切线;(2)、若OE=1,CD=2,求 的长.
(1)、求证:PA是⊙O的切线;(2)、若OE=1,CD=2,求 的长. -
23. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出A型和B型两款垃圾分拣机器人,已知2台A型机器人和5台B型机器人同时工作2小时共分拣垃圾3.6吨,3台A型机器人和2台B型机器人同时工作5小时共分拣垃圾8吨.(1)、1台A型机器人和1台B型机器人每小时各分拣垃圾多少吨?(2)、某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人,机器人公司的报价如下表:
型号
原价
购买量少于30台
购买量不少于30台
A型
20万元/台
原价购买
打九折
B型
12万元/台
原价购买
打八折
①若要求这批机器人每小时一共能分拣垃圾20吨.设其中购买A型机器人x台(10≤x≤35),购买两种机器人总费用为W万元.求W与x的函数关系式,并说明如何购买总费用最少;
②为了加快垃圾分拣速度,垃圾处理厂计划用不超过140万元增购这两种机器人共10台,机器人公司全部以打折后价格销售,这10台机器人每小时最多处理多少吨垃圾?
-
24. 在矩形ABCD中, (k为常数),点P是对角线BD上一动点(不与B,D重合),将射线PA绕点P逆时针旋转90°与射线CB交于点E,连接AE.
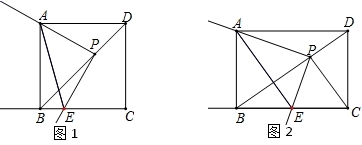 (1)、特例发现:如图1,当k=1时,将点P移动到对角线交点处,可发现点E与点B重合,则 = , ∠AEP=;当点P移动到其它位置时,∠AEP的大小(填“改变”或“不变”);(2)、类比探究:如图2,若k≠1时,当k的值确定时,请探究∠AEP的大小是否会随着点P的移动而发生变化,并说明理由;(3)、拓展应用:当k≠1时,如图2,连接PC,若PC⊥BD, ,PC=2,求AP的长.
(1)、特例发现:如图1,当k=1时,将点P移动到对角线交点处,可发现点E与点B重合,则 = , ∠AEP=;当点P移动到其它位置时,∠AEP的大小(填“改变”或“不变”);(2)、类比探究:如图2,若k≠1时,当k的值确定时,请探究∠AEP的大小是否会随着点P的移动而发生变化,并说明理由;(3)、拓展应用:当k≠1时,如图2,连接PC,若PC⊥BD, ,PC=2,求AP的长. -
25. 在平面直角坐标系中,抛物线解析式为 ,直线l:y=-x+1与x轴交于点A,与y轴交于点B.
 (1)、如图1,当抛物线经过点A且与x轴的两个交点都在y轴右侧时,求抛物线的解析式.(2)、在(1)的条件下,若点P为直线l上方的抛物线上一点,过点P作PQ⊥l于Q,求PQ的最大值.(3)、如图2,点C(-2,0),若抛物线与线段AC只有一个公共点,求m的取值范围.
(1)、如图1,当抛物线经过点A且与x轴的两个交点都在y轴右侧时,求抛物线的解析式.(2)、在(1)的条件下,若点P为直线l上方的抛物线上一点,过点P作PQ⊥l于Q,求PQ的最大值.(3)、如图2,点C(-2,0),若抛物线与线段AC只有一个公共点,求m的取值范围.
