湖北省荆州市2021年数学中考模拟试卷
试卷更新日期:2021-08-03 类型:中考模拟
一、单选题
-
1. 在实数 ,1,0,-3中,无理数是( )A、 B、1 C、0 D、-32. 把一块直尺与一块三角板如图放置,若 ,则 的度数为( )
 A、40° B、50° C、140° D、130°3. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
A、40° B、50° C、140° D、130°3. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )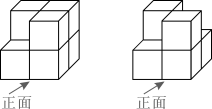 A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同4. 用换元法解方程 时,若设 ,则原方程可化为关于 的方程是( )A、 B、 C、 D、5. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同4. 用换元法解方程 时,若设 ,则原方程可化为关于 的方程是( )A、 B、 C、 D、5. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
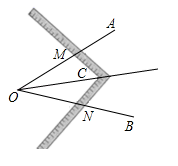 A、SSS B、SAS C、ASA D、AAS6. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、7. 解方程组 时,用含 的代数式表示 的值为( )A、 B、 C、 D、8. 如图, 中, ,根据尺规作图的痕迹判断以下结论错误的是( )
A、SSS B、SAS C、ASA D、AAS6. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、7. 解方程组 时,用含 的代数式表示 的值为( )A、 B、 C、 D、8. 如图, 中, ,根据尺规作图的痕迹判断以下结论错误的是( )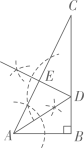 A、 B、 C、 D、9. 如图,直径为10的⊙A经过点 和点 ,点 是 轴右侧⊙A优弧上一点, ,则点 的坐标为( )
A、 B、 C、 D、9. 如图,直径为10的⊙A经过点 和点 ,点 是 轴右侧⊙A优弧上一点, ,则点 的坐标为( ) A、 B、 C、 D、10. 直线 不经过第二象限,则关于 的方程 实数解的个数是( ).A、0个 B、1个 C、2个 D、1个或2个
A、 B、 C、 D、10. 直线 不经过第二象限,则关于 的方程 实数解的个数是( ).A、0个 B、1个 C、2个 D、1个或2个二、填空题
-
11. 化简 的结果是.12. 上电脑课时,有一排桌上放有四台电脑,同学 先坐在如图的一台电脑前的座位上, , , 三位同学随机坐到其他三个座位上,则 与B两同学坐在相邻电脑前座位上的概率为.
 13. 如图,将一块含30°角的直角三角板和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积为 . (结果保留π)
13. 如图,将一块含30°角的直角三角板和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积为 . (结果保留π) 14. 如图,某天然气公司的主输气管道从 市的北偏东60°方向直线延伸,测绘员在 处测得要安装天然气的 小区在 市北偏东30°方向,测绘员沿主输气管道步行2000米到达 处,测得小区 位于 的北偏西60°方向.当在主输气管道 上寻找支管道连接点 ,使到该小区 铺设的管道最短时, 的长为.
14. 如图,某天然气公司的主输气管道从 市的北偏东60°方向直线延伸,测绘员在 处测得要安装天然气的 小区在 市北偏东30°方向,测绘员沿主输气管道步行2000米到达 处,测得小区 位于 的北偏西60°方向.当在主输气管道 上寻找支管道连接点 ,使到该小区 铺设的管道最短时, 的长为.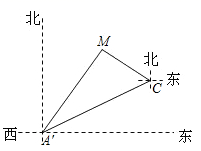 15. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.
15. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为. 16. 如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作 ( 为1~8的整数).函数 的图象为曲线 .若 过点 ,则它必定还过另一点 ,则 .
16. 如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作 ( 为1~8的整数).函数 的图象为曲线 .若 过点 ,则它必定还过另一点 ,则 .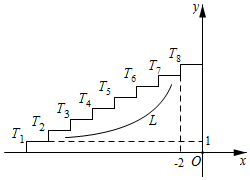
三、解答题
-
17. 若计算 的结果为 ,请估算 的值最接近于哪两个整数之间.18. 若关于 的一元一次不等式组 的解集是 ,求关于 的分式方程 的非负整数解.19. 如图,方格纸中每个小正方形的边长为1,线段AB和线段CD的端点均在小正方形的顶点上.
 (1)、在图中画出以AB为边的正方形 ,点E和点F均在小正方形的顶点上;(2)、在图中画出以CD为边的等腰三角形 ,点G在小正方形的顶点上,且 的周长为 ,连接EG,请直接写出线段EG的长.20. 每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;八年级10名学生的竞赛成绩在C组中的数据是:94,90,94.七、八年级抽取的学生竞赛成绩统计表
(1)、在图中画出以AB为边的正方形 ,点E和点F均在小正方形的顶点上;(2)、在图中画出以CD为边的等腰三角形 ,点G在小正方形的顶点上,且 的周长为 ,连接EG,请直接写出线段EG的长.20. 每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;八年级10名学生的竞赛成绩在C组中的数据是:94,90,94.七、八年级抽取的学生竞赛成绩统计表年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4

根据以上信息,解答下列问题:
(1)、直接写出上述图表中a,b,c的值;(2)、根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);(3)、该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥90)的学生人数是多少?21. 函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数 和 的图象如图所示.x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
﹣6
﹣4
﹣2
0
﹣2
﹣4
﹣6
…
 (1)、观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数 的对称轴.(2)、探索思考:平移函数 的图象可以得到函数 和 的图象,分别写出平移的方向和距离.(3)、拓展应用:在所给的平面直角坐标系内画出函数 的图象.若点 和 在该函数图象上,且 ,比较 , 的大小.22. 一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
(1)、观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数 的对称轴.(2)、探索思考:平移函数 的图象可以得到函数 和 的图象,分别写出平移的方向和距离.(3)、拓展应用:在所给的平面直角坐标系内画出函数 的图象.若点 和 在该函数图象上,且 ,比较 , 的大小.22. 一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:销售单价x(元/kg)
120
130
…
180
每天销量y(kg)
100
95
…
70
设y与x的关系是我们所学过的某一种函数关系.
(1)、直接写出y与x的函数关系式,并指出自变量x的取值范围;(2)、当销售单价为多少时,销售利润最大?最大利润是多少?23. 如图1,在 中, , , 是等边三角形, 是 的中点,连接 并延长交 于 .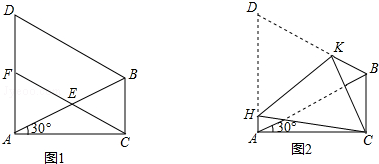 (1)、求证:① ;② ;(2)、如图2,将四边形 折叠,使 与 重合, 为折痕,求 的值.24. 如图1,解析式为 的直线 与 , 轴分别相交于 , 两点,将 绕点 逆时针旋转90°得到 ,过点 , , 的抛物线 叫做 的关联抛物线,而 叫做 的关联直线.
(1)、求证:① ;② ;(2)、如图2,将四边形 折叠,使 与 重合, 为折痕,求 的值.24. 如图1,解析式为 的直线 与 , 轴分别相交于 , 两点,将 绕点 逆时针旋转90°得到 ,过点 , , 的抛物线 叫做 的关联抛物线,而 叫做 的关联直线.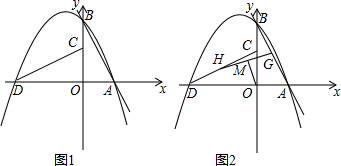 (1)、①若 的解析式为 ,求 表示的函数解析式;
(1)、①若 的解析式为 ,求 表示的函数解析式;②若 的解析式为 ,求 表示的函数解析式;
(2)、求 的对称轴(用含 , 的代数式表示);(3)、如图2,若 的解析式为 , 为 中点, 为 中点,连接 , 为 中点,连接 .若 ,真接写出 , 表示的函数解析式.