湖北省荆门市2021年数学学业水平适应性考试试卷
试卷更新日期:2021-08-03 类型:中考模拟
一、单选题
-
1. 实数 的绝对值是( )A、2 B、 C、 D、2. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、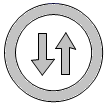 D、
D、 3. 根据美国约翰斯·霍普金斯大学于美国东部时间4月10日18时16分(北京时间4月11日6时16分)统计的数据显示,美国新冠肺炎累计确诊病例已超过3114万例,达到31145168例.将数字3114万用科学记数法表示应为( )A、 B、 C、 D、4. 如图所示,该几何体的俯视图是( )
3. 根据美国约翰斯·霍普金斯大学于美国东部时间4月10日18时16分(北京时间4月11日6时16分)统计的数据显示,美国新冠肺炎累计确诊病例已超过3114万例,达到31145168例.将数字3114万用科学记数法表示应为( )A、 B、 C、 D、4. 如图所示,该几何体的俯视图是( ) A、
A、 B、
B、 C、
C、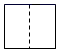 D、
D、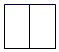 5. 小明在学习平行线的性质后,把含有60°角的直角三角板摆放在自己的文具上,如图,AD∥BC,若∠2=70°,则∠1=( )
5. 小明在学习平行线的性质后,把含有60°角的直角三角板摆放在自己的文具上,如图,AD∥BC,若∠2=70°,则∠1=( ) A、22° B、20° C、25° D、30°6. 下列运算正确的是( )A、 B、 C、 D、7. 《九章算术》是我国古代数学的经典著作,奠定了中国传统数学的基本框架,书中记载:“今有大器五、小器一容三斛;大器一、小器五容二斛,问大小器各容几何?”译文:“今有大容器5个、小容器1个,总容量为3斛;大容器1个、小容器5个,总容量为2斛.问大小容器的容积各是多少斛?”设1个大容器的容积为 斛,1个小容器的容积 斛,则根据题意可列方程组( )A、 B、 C、 D、8. 如图, 是等边三角形, 是等腰三角形,且 ,过点 作 的平行线交 于点 ,若 , ,则 的长为( )
A、22° B、20° C、25° D、30°6. 下列运算正确的是( )A、 B、 C、 D、7. 《九章算术》是我国古代数学的经典著作,奠定了中国传统数学的基本框架,书中记载:“今有大器五、小器一容三斛;大器一、小器五容二斛,问大小器各容几何?”译文:“今有大容器5个、小容器1个,总容量为3斛;大容器1个、小容器5个,总容量为2斛.问大小容器的容积各是多少斛?”设1个大容器的容积为 斛,1个小容器的容积 斛,则根据题意可列方程组( )A、 B、 C、 D、8. 如图, 是等边三角形, 是等腰三角形,且 ,过点 作 的平行线交 于点 ,若 , ,则 的长为( )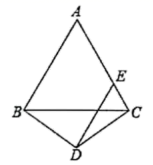 A、6 B、 C、 D、9. 如图,点 为 的内心, , , ,则 的面积是( )
A、6 B、 C、 D、9. 如图,点 为 的内心, , , ,则 的面积是( ) A、 B、 C、2 D、410. 已知抛物线 与 轴最多有一个交点,其顶点为 ,有下列结论:① ;② ;③关于 的方程 无实数根;④ 的最大值为-3.其中,正确结论的个数为( )A、4个 B、3个 C、2个 D、1个
A、 B、 C、2 D、410. 已知抛物线 与 轴最多有一个交点,其顶点为 ,有下列结论:① ;② ;③关于 的方程 无实数根;④ 的最大值为-3.其中,正确结论的个数为( )A、4个 B、3个 C、2个 D、1个二、填空题
-
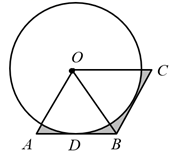
11. 计算 .12. 不等式组 的解集是.13. 如图,在菱形 中, 是对角线, ,⊙O与边 相切于点D,则图中阴影部分的面积为 .
 14. 如图,矩形 的顶点 在双曲线 上, , 两点分别在 轴, 轴的正半轴上,将矩形 绕点 顺时针旋转90°,得到矩形 ,边 , 分别交此双曲线于 , 两点,若 , 的面积为1,则 .
14. 如图,矩形 的顶点 在双曲线 上, , 两点分别在 轴, 轴的正半轴上,将矩形 绕点 顺时针旋转90°,得到矩形 ,边 , 分别交此双曲线于 , 两点,若 , 的面积为1,则 . 15. 如图,在正方形 中, 与 交于点 是 的中点,点 在 边上,且 为对角线 上一点, 则 的最大值为 .
15. 如图,在正方形 中, 与 交于点 是 的中点,点 在 边上,且 为对角线 上一点, 则 的最大值为 .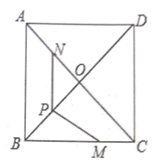 16. 如图,已知直线 和直线 ,过 上的点 作 轴的平行线交 于点 ,过点 作 轴的平行线交 于点 ,过点 作 轴的平行线交 于点 ,…,按此作法进行下去,则点 的横坐标为.
16. 如图,已知直线 和直线 ,过 上的点 作 轴的平行线交 于点 ,过点 作 轴的平行线交 于点 ,过点 作 轴的平行线交 于点 ,…,按此作法进行下去,则点 的横坐标为.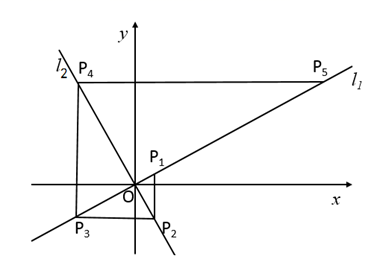
三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图,将矩形纸片 沿 折叠,使点 与点 重合.
 (1)、求证: ;(2)、若 , ,求 的长.19. 某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组: ; ; ; ,并绘制出如图不完整的统计图.
(1)、求证: ;(2)、若 , ,求 的长.19. 某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组: ; ; ; ,并绘制出如图不完整的统计图.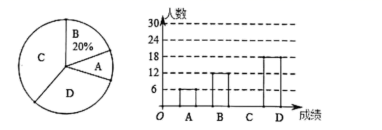
解答下列问题:
(1)、求被抽取的学生成绩在 组的有多少人?(2)、所抽取学生成绩的中位数落在哪个组内?(3)、学校要将D组最优秀的4名学生分成两组,每组2人到不同的社区进行“交通法规”知识演讲.已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,求九年级的2名学生恰好分在同一个组的概率.20. 如图,某天我国一艘海监船巡航到 港口正西方的 处时,发现在 的北偏东60°方向,相距150海里的 处有一可疑船只正沿 方向行驶,点 在 港口的北偏东30°方向上,海监船向 港口发出指令,执法船立即从 港口沿 方向驶出,在 处成功拦截可疑船只,此时点 与点 的距离为 海里. (1)、求点 到直线 的距离.(2)、执法船从 到 航行了多少海里?21. 已知 , 是一元二次方程 的两个实数根.(1)、求 的取值范围;(2)、是否存在实数 ,使得等式 成立?如果存在,求出 的值;如果不存在,请说明理由.22. 如图1,点 在以 为直径的 上, 是 延长线上一点, ,过点 作 ,垂足为 ,交 于点 .
(1)、求点 到直线 的距离.(2)、执法船从 到 航行了多少海里?21. 已知 , 是一元二次方程 的两个实数根.(1)、求 的取值范围;(2)、是否存在实数 ,使得等式 成立?如果存在,求出 的值;如果不存在,请说明理由.22. 如图1,点 在以 为直径的 上, 是 延长线上一点, ,过点 作 ,垂足为 ,交 于点 .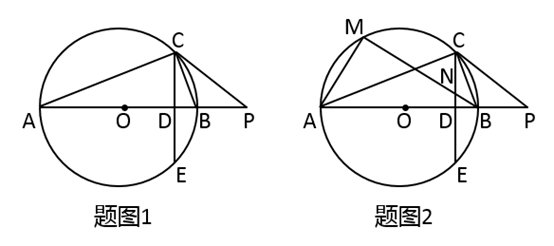 (1)、求证: 是 的切线:(2)、若点 是 的中点,求 的度数;(3)、如图2,过点 作 交 于点 ,交 于点 ,连接 .若 , ,求 的长.23. 某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
(1)、求证: 是 的切线:(2)、若点 是 的中点,求 的度数;(3)、如图2,过点 作 交 于点 ,交 于点 ,连接 .若 , ,求 的长.23. 某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:x(天)
1
2
3
…
m(kg)
20
24
28
…
 (1)、请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式(2)、求在销售的第几天时,当天的利润最大,最大利润是多少?(3)、请求出试销的20天中当天的销售利润不低于1680元的天数.24. 如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,且 ,连接 ,直线 与 轴交于点 ,与 上方的抛物线交于点 ,与 交于点 .
(1)、请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式(2)、求在销售的第几天时,当天的利润最大,最大利润是多少?(3)、请求出试销的20天中当天的销售利润不低于1680元的天数.24. 如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,且 ,连接 ,直线 与 轴交于点 ,与 上方的抛物线交于点 ,与 交于点 . (1)、求点 , 的坐标及抛物线的解析式;(2)、设 的面积为 , 的面积为 ,当 最大时,求 的值:(3)、在(2)的条件下,点 是抛物线上一点,点 是直线 上一点,是否存在以 , , , 为顶点的四边形是平行四边形,若存在,直接写出点 的坐标;若不存在,请说明理由.
(1)、求点 , 的坐标及抛物线的解析式;(2)、设 的面积为 , 的面积为 ,当 最大时,求 的值:(3)、在(2)的条件下,点 是抛物线上一点,点 是直线 上一点,是否存在以 , , , 为顶点的四边形是平行四边形,若存在,直接写出点 的坐标;若不存在,请说明理由.