湖北省大冶市2021年数学中考二模试卷
试卷更新日期:2021-08-03 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 下列图形中,是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个3. 如图所示的几何体,其俯视图是( )
A、1个 B、2个 C、3个 D、4个3. 如图所示的几何体,其俯视图是( )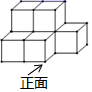 A、
A、 B、
B、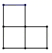 C、
C、 D、
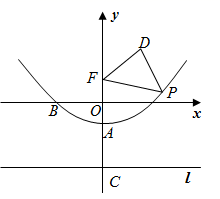
D、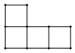 4. 下列计算正确的是( )A、 + = B、x6÷x3=x2 C、 =2 D、a2(﹣a2)=a45. 要使式子 有意义,则 的取值范围是( )A、 且 B、 C、 D、6. 一组数据为x,2,4,10,14,8.若这组数据的众数为10,则这组数据的中位数为( )A、7 B、8 C、9 D、107. 如图,在平面直角坐标系 中,点 的坐标为 ,点A的坐标为(1,0),将线段 绕点 顺时针旋转 得到线段 ,则点 的坐标为( )
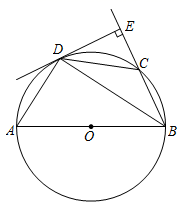
4. 下列计算正确的是( )A、 + = B、x6÷x3=x2 C、 =2 D、a2(﹣a2)=a45. 要使式子 有意义,则 的取值范围是( )A、 且 B、 C、 D、6. 一组数据为x,2,4,10,14,8.若这组数据的众数为10,则这组数据的中位数为( )A、7 B、8 C、9 D、107. 如图,在平面直角坐标系 中,点 的坐标为 ,点A的坐标为(1,0),将线段 绕点 顺时针旋转 得到线段 ,则点 的坐标为( ) A、 B、 C、 D、8. 如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
A、 B、 C、 D、8. 如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( ) A、80° B、100° C、110° D、130°9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( )
A、80° B、100° C、110° D、130°9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( ) A、 B、3 C、4 D、510. 如图是二次函数 的图象的一部分,图象过点 ,二次函数的对称轴为 ,给出下列结论:① ;② ;③ ;④ ;⑤当 时, ,其中正确的是( )
A、 B、3 C、4 D、510. 如图是二次函数 的图象的一部分,图象过点 ,二次函数的对称轴为 ,给出下列结论:① ;② ;③ ;④ ;⑤当 时, ,其中正确的是( ) A、②③⑤ B、①③ C、②③ D、①④⑤
A、②③⑤ B、①③ C、②③ D、①④⑤二、填空题
-
11. 计算: .12. 因式分解 的结果是.13. 习总书记提出“生态兴则文明兴”、“守住绿水青山,就是守住金山银山”,人人都有爱护环境的义务.某时刻在无锡监测点监测到PM 2.5的含量为65微克/米3 , 即0.000065克/米3 , 将0.000065用科学记数法表示为 .14. 如图,在半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为.
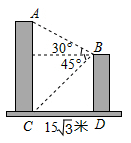
 15. 如图,某校教学楼 与实验楼 的水平间距 米,在实验楼顶部 点测得教学楼顶部 点的仰角是 ,底部 点的俯角是 ,则教学楼 的高度是米(结果保留根号).
15. 如图,某校教学楼 与实验楼 的水平间距 米,在实验楼顶部 点测得教学楼顶部 点的仰角是 ,底部 点的俯角是 ,则教学楼 的高度是米(结果保留根号).
 16. 已知函数 ,当 时,y有最大值6,则 .17. 如图,一直线经过原点 ,且与反比例函数 相交于点 、点 ,过点 作 轴,垂足为 ,连接 .若 面积为 ,则 .
16. 已知函数 ,当 时,y有最大值6,则 .17. 如图,一直线经过原点 ,且与反比例函数 相交于点 、点 ,过点 作 轴,垂足为 ,连接 .若 面积为 ,则 .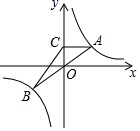 18. 如图,在 中, , 、 是斜边 上两点,且 ,将 绕点 顺时针旋转90°后,得到 ,连接 ,下列结论:① ;② ;③ ;④ ,其中正确的结论有个.
18. 如图,在 中, , 、 是斜边 上两点,且 ,将 绕点 顺时针旋转90°后,得到 ,连接 ,下列结论:① ;② ;③ ;④ ,其中正确的结论有个.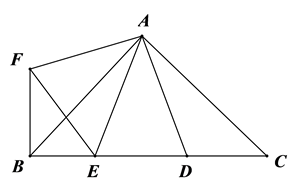
三、解答题
-
19. 先化简,再求值: ,其中 .20. 如图, ,直线 过点 , 直线 , 直线 ,垂足分别为 、 ,且 .
 (1)、求证 ;(2)、求证 .21. 若关于 的方程 有两个实数根.(1)、求 的取值范围;(2)、若方程的两根 , ,满足 ,求 的值.22. 每年5月的第二周为:“职业教育活动周”,今年某市开展了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).
(1)、求证 ;(2)、求证 .21. 若关于 的方程 有两个实数根.(1)、求 的取值范围;(2)、若方程的两根 , ,满足 ,求 的值.22. 每年5月的第二周为:“职业教育活动周”,今年某市开展了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).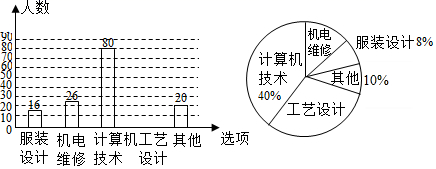 (1)、补全条形统计图;(2)、若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?(3)、要从这些被调查的学生中随机抽取一人进行访谈,求正好抽到对“机电维修”最感兴趣的学生的概率.23. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任,某小区购进A型和B型两种分类垃圾桶,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花20元,购买A型、B型垃圾桶各花费了1000元,且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍.(1)、求购买一个A型垃圾桶和一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型和B型垃圾桶共60个,要使总费用不超过2000元,最少要购买多少个A型垃圾桶?
(1)、补全条形统计图;(2)、若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?(3)、要从这些被调查的学生中随机抽取一人进行访谈,求正好抽到对“机电维修”最感兴趣的学生的概率.23. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任,某小区购进A型和B型两种分类垃圾桶,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花20元,购买A型、B型垃圾桶各花费了1000元,且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍.(1)、求购买一个A型垃圾桶和一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型和B型垃圾桶共60个,要使总费用不超过2000元,最少要购买多少个A型垃圾桶?