云南省大理白族自治州祥云县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2021-08-03 类型：期末考试

进入出卷网下载

一、填空题

1. 一元二次方程 $3 x^{2} = x$ 的根是.

查看试题解析
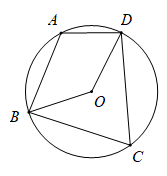
2. 二次函数y= $- 2 {(x - 2)}^{2} + 1$ 的对称轴为．

查看试题解析
3. 如图，四边形ABCD是⊙O的内接四边形，若∠BOD＝130°，则∠A＝．

查看试题解析
4. 圆锥的侧面展开图的圆心角是120°，其底面圆的半径为2cm，则其侧面展开图的半径为cm．

查看试题解析
5. 将抛物线 $y = {(x + 2)}^{2} - 1$ 先向上平移2个单位，再向左平移1个单位后，得到的抛物线解析式为．

查看试题解析
6. 给出下列函数① $y = 3 x + 1$ ；② $y = - 2 x$ ；③ $y = - \frac{1}{5} x^{2}$ ．从中任取一个函数，则取出的函数符合条件“当 $x > 1$ 时，函数值 $y$ 随 $x$ 的增大而减小”的概率是．

查看试题解析

二、单选题

7. 下列图形既是轴对称图形，又是中心对称图形的是（）

A、 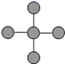B、 C、 D、

查看试题解析
8. 用配方法解一元二次方程 $x^{2} - 6 x - 1 = 0$ ，下列变形正确的是（）

A、 ${(x - 6)}^{2} = 35$ B、 ${(x - 6)}^{2} = 37$ C、 ${(x - 3)}^{2} = 8$ D、 ${(x - 3)}^{2} = 10$

查看试题解析
9. 若正六边形的半径长为4，则它的边长等于（）

A、4 B、2 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
10. 已知方程3x²-2x-4=0的两根分别为x₁和x₂ ，则x₁+x₂的值为（）

A、- $\frac{2}{3}$ B、 $\frac{2}{3}$ C、- $\frac{4}{3}$ D、 $\frac{4}{3}$

查看试题解析
11. 如图，已知AB是⊙O的弦，⊙O的半径OC⊥AB于点 D，交⊙O于点C，且CD = 2，AB=8则⊙O的半径长为（）

A、4 B、5 C、6 D、7

查看试题解析
12. 如图，平面直角坐标系中，AB⊥x轴于点B ，点A的坐标为（ $2 \sqrt{3}$ ，2），将△AOB绕原点O顺时针旋转90°得到△A´OB´，则A´的坐标是（）

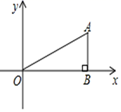A、（2，- $2 \sqrt{3}$ ） B、（ $2 \sqrt{3}$ ， 2 ） C、（﹣2， $2 \sqrt{3}$ ） D、（ $2 \sqrt{3}$ ，﹣2）

查看试题解析
13. 下列事件是必然事件的是（）．

A、购买一张彩票中奖 B、通常加热到100℃时，水沸腾 C、明天一定是晴天 D、任意一个三角形，其内角和是360°

查看试题解析
14. 如图，已知二次函数y＝ax²+bx+c（a≠0）的图象．下列结论：①abc＜0；②a-b+c＜0；③ax²+bx+c＝0有两个实数根；④2a-b=0．其中正确的个数是（）

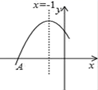A、4 B、3 C、2 D、1

查看试题解析

三、解答题

15. 计算：

(1)、 $y^{2} - 2 y + 1 = 25$

(2)、 $x^{2} - 4 x - 3 = 0$

查看试题解析
16. 已知关于x的一元二次方程x²-6x+2m-1=0有两个相等的实数根，求m的值及方程的根

查看试题解析
17. 如图

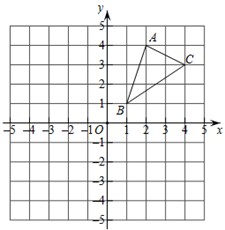
（1）请画出△ABC关于原点O对称的△A₁B₁C₁；
（2）请画出△ABC绕点B逆时针旋转90°后的△A₂BC₂；
（3）写出A₂和C₂两点坐标．

查看试题解析
18. 在不透明的口袋里装分别标有数字1、2、3的三个乒乓球(除数字外其余都相同) ，第一次任意摸一个球（不放回），将小球上的数字作为横坐标，然后第二次再摸一个球，将小球上的数字作为纵坐标．

(1)、求所有等可能的点的坐标；

(2)、请用画树状图或列表格法，求出点在函数 $y = x^{2} + 1$ 图像上的概率．

查看试题解析
19. 如图，在平面直角坐标系中，已知⊙D经过原点O ，与x轴、y轴分别交于A、B两点，B点坐标为（0，2 $\sqrt{3}$ ），OC与⊙D交于点C ， ∠OCA＝30°．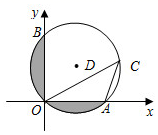

(1)、求⊙D的半径；

(2)、求圆中阴影部分的面积（结果保留根号和π）．

查看试题解析
20. 某服装批发市场经销一种品牌衬衫，如果每件盈利10元，每天可卖500件．经市场调查发现，在进货价不变的情况下，若每件涨价1元，日销售量将减少20件．当每件衬衫涨价多少元时，既能保证批发商每日盈利6000元，又能使顾客得到实惠？

查看试题解析
21. 已知AB是⊙O的切线，切点为B点，AO交⊙O于点C，点D在AB上且DB=DC．

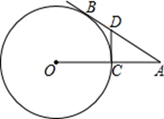(1)、求证：DC为⊙O的切线；

(2)、当AD=2BD，CD=2时，求AO的长．

查看试题解析
22. 某种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价 $x$ （元）之间的关系可以近似地看作一次函数 $y = - 2 x + 100$ ．

(1)、写出每月的利润W（万元）与销售单价 $x$ （元）之间的函数关系式；

(2)、物价部门规定该产品销售单价不低于成本且不高于33元．当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？

查看试题解析
23. 如图，已知抛物线y=ax²+bx+c与x轴相交于A、B两点，与y轴相交于点C（0，3），且OA=1，OB=3．

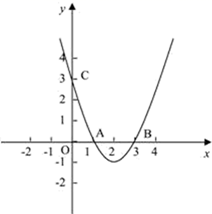(1)、求抛物线的函数关系式；

(2)、若点D（4，3）是抛物线y=ax²+bx+c上的一点，那么在抛物线的对称轴上，是否存在一点P，使得△BDP的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析