云南省大理白族自治州2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-08-03 类型:期末考试
一、填空题
-
1. 点M(1,-2)关于原点对称点的坐标是.2. 将抛物线 向左平移2个单位长度,再向下平移5个单位长度,得到抛物线的解析式是 .3. 关于 的一元二次方程 有实数根,则实数 的取值范围是.4. 用半径为6,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为.5. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.点P为y轴上一点,连接PA,PC,则 的面积为 .
 6. 在平面直角坐标系中, 和 的相似比等于 ,并且是关于原点O的位似图形,若点A的坐标为 ,则其对应点 的坐标是 .
6. 在平面直角坐标系中, 和 的相似比等于 ,并且是关于原点O的位似图形,若点A的坐标为 ,则其对应点 的坐标是 .二、单选题
-
7. 我国汽车工业迅速发展,国产汽车技术成熟,下列汽车图标是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
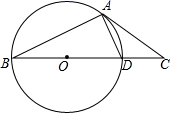
D、 8. 下列说法中错误的是( )A、篮球队员在罚球线上投篮一次,未投中是随机事件 B、“任意画出一个平行四边形,它是中心对称图形”是必然事件 C、“抛一枚硬币,正面向上的概率为 ”表示每抛两次就有一次正面朝上 D、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近9. 如图,已知 是 的直径, 是弦,若 则 等于( )
8. 下列说法中错误的是( )A、篮球队员在罚球线上投篮一次,未投中是随机事件 B、“任意画出一个平行四边形,它是中心对称图形”是必然事件 C、“抛一枚硬币,正面向上的概率为 ”表示每抛两次就有一次正面朝上 D、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近9. 如图,已知 是 的直径, 是弦,若 则 等于( ) A、 B、 C、 D、10. 如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )
A、 B、 C、 D、10. 如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )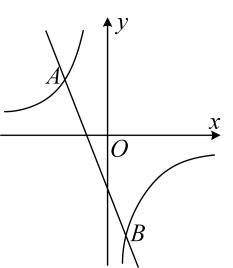 A、 B、 或 C、 D、 或11. 如图是一块三角形钢材ABC,其中边 ,高 ,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A、 B、 或 C、 D、 或11. 如图是一块三角形钢材ABC,其中边 ,高 ,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( ) A、16 B、24 C、30 D、3612. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式 ,则最佳加工时间为( )min.A、2 B、5 C、2或5 D、3.513. 如图,在边长为1的正六边形 中,M是边 上一点,则线段 的长可以是( )
A、16 B、24 C、30 D、3612. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式 ,则最佳加工时间为( )min.A、2 B、5 C、2或5 D、3.513. 如图,在边长为1的正六边形 中,M是边 上一点,则线段 的长可以是( ) A、1.4 B、1.6 C、1.8 D、2.214. 如图,已知二次函数 的图象如图所示,有下列5个结论 ; ; ; ; 的实数 其中正确结论的有( )
A、1.4 B、1.6 C、1.8 D、2.214. 如图,已知二次函数 的图象如图所示,有下列5个结论 ; ; ; ; 的实数 其中正确结论的有( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
15. 解下列一元二次方程:(1)、(2)、16. 如图,在平面直角坐标系中, 三个顶点的坐标分别为 , , .

(1)请画出 关于原点对称的 ;
(2)请画出 绕点B逆时针旋转90°后的 ,求点A到 所经过的路径长.17. 某口罩生产厂生产的口罩1月份平均日产量为20000,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月份平均日产量达到24200个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计4月份平均日产量为多少?18. 随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学,某校复学后成立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.(1)、李老师被分配到“洗手监督岗”的概率为(2)、用列表法或面树状图法,求李老师和王老师被分配到同一个监督岗的概率.19. 已知反比例函数 的图象经过点 ,点(1)、求k及m的值.(2)、点 , 均在反比例函数 的图象上,若 ,比较 , 的大小关系.20. 某超市销售一款“免洗洗手液”,这款“免洗洗手液”的成本价为每瓶16元,当销售单价定为20元时,每天可售出80瓶.根据市场行情,现决定降价销售.市场调查反映:销售单价每降低0.5元,则每天可多售出20瓶(销售单价不低于成本价),若设这款“免洗洗手液”的销售单价为x(元),每天的销售量为y(瓶).(1)、求每天的销售量y(瓶)与销售单价x(元)之间的函数关系式;(2)、当销售单价为多少元时,销售这款“免洗洗手液”每天的销售利润最大,最大利润为多少元?