辽宁省协作校2020-2021学年高二下学期数学期末考试试卷
试卷更新日期:2021-08-03 类型:期末考试
一、单选题
-
1. 已知: ,则 ( )A、 B、 C、 D、2. 同时抛掷两枚硬币,则两枚硬币一枚正面向上一枚反面向上的概率是( ).A、 B、 C、 D、3. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件4. 下列命题错误的是( )A、若平面 平面 ,则平面 内所有直线都垂直于平面 B、若平面 平面 ,则平面 内一定存在直线垂直于平面 C、若平面 不垂直于平面 ,则平面 内一定不存在直线垂直于平面 D、若平面 平面 ,平面 平面 , ,则5. 已知递增等比数列 中, , ,若 ,则 ( ).A、5 B、6 C、7 D、86. 三个数 , , 之间的大小关系是( )A、 B、 C、 D、7. 函数 的图象大致为( )A、
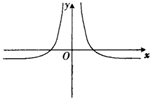 B、
B、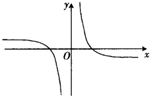 C、
C、 D、
D、 8. 原始的蚊香出现在宋代.根据宋代《格物粗谈》记载:“端午时,贮浮萍,阴干,加雄黄,作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用数学软件制作的“螺旋蚊香”,画法如下:在水平直线 上取长度为1的线段 ,做一个等边三角形 ,然后以点 为圆心, 为半径逆时针画圆弧,交线段 的延长线于点 ,再以点 为圆心, 为半径逆时针画圆弧,交线段 的延长线于点 ,以此类推,则如图所示的“螺旋蚊香”的总长度为( ).
8. 原始的蚊香出现在宋代.根据宋代《格物粗谈》记载:“端午时,贮浮萍,阴干,加雄黄,作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用数学软件制作的“螺旋蚊香”,画法如下:在水平直线 上取长度为1的线段 ,做一个等边三角形 ,然后以点 为圆心, 为半径逆时针画圆弧,交线段 的延长线于点 ,再以点 为圆心, 为半径逆时针画圆弧,交线段 的延长线于点 ,以此类推,则如图所示的“螺旋蚊香”的总长度为( ). A、 B、 C、 D、9. 执行如图的程序框图,若输出的 ,则输入的整数 的最小值是
A、 B、 C、 D、9. 执行如图的程序框图,若输出的 ,则输入的整数 的最小值是 A、4 B、5 C、6 D、1510. 已知角 满足 ,则 ( )A、 B、 C、 D、11. 椭圆 的左右焦点分别是 , ,以 为圆心的圆过椭圆的中心,且与椭圆交于点 ,若直线 恰好与圆 相切于点 ,则椭圆的离心率为( )A、 B、 C、 D、12. 设函数 ,其中 ,若有且只有一个整数 使得 ,则 的取值范围是( )A、 B、 C、 D、
A、4 B、5 C、6 D、1510. 已知角 满足 ,则 ( )A、 B、 C、 D、11. 椭圆 的左右焦点分别是 , ,以 为圆心的圆过椭圆的中心,且与椭圆交于点 ,若直线 恰好与圆 相切于点 ,则椭圆的离心率为( )A、 B、 C、 D、12. 设函数 ,其中 ,若有且只有一个整数 使得 ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 在平面直角坐标系中,将曲线 上每一点的横坐标变为原来的2倍,纵坐标保持不变,所得新的曲线的方程为 .14. 已知向量 =(-4,3), =(6,m),且 ,则m=.15. 抛物线 的焦点为 ,已知抛物线在 点处的切线斜率为2,则直线 与该切线的夹角的正弦值为 .16. 已知一族双曲线 ,设直线 与 在第一象限内的交点为 ,点 在 的两条渐近线上的射影分别为 、 ,记 的面积为 ,对任意 不等式 恒成立,则 的最小值为 .
三、解答题
-
17. 某同学用“五点法”画函数 在某一个周期内的图像时,列表并填入了部分数据,如表:
0
0
2
0
0
(1)、根据表中数据求函数 的解析式;(2)、求函数 在区间 上的最大值和最小值.18. 2021年是中国共产党成立100周年,中共中央要求我们要熟悉党史、学习党史.某社区为了解居民对党史的认知情况,举行了一次党史知识竞赛,并从所有的居民竞赛试卷中随机抽取n份试卷进行成绩分析,得到成绩频率分布直方图(如图所示),其中成绩在 的试卷份数是24. (1)、求 , 的值;(2)、用分层抽样的方法在成绩为 和 这两组中共抽取5份试卷,并从这5份试卷中任取2份试卷的居民进行点评,求分数在 恰有1份的概率.19. 如图,在三棱锥 中,平面 平面 , , , .
(1)、求 , 的值;(2)、用分层抽样的方法在成绩为 和 这两组中共抽取5份试卷,并从这5份试卷中任取2份试卷的居民进行点评,求分数在 恰有1份的概率.19. 如图,在三棱锥 中,平面 平面 , , , . (1)、求证 ;(2)、求二面角 的余弦值.20. 已知椭圆 以直线 所过的定点为一个焦点,且短轴长为4.(1)、求椭圆 的标准方程;(2)、已知椭圆 的中心在原点,焦点在 轴上,且长轴和短轴的长分别是椭圆 的长轴和短轴的长的 倍 ,过点 的直线 与椭圆 交于 , 两个不同的点,若 ,求 的面积的最大值.
(1)、求证 ;(2)、求二面角 的余弦值.20. 已知椭圆 以直线 所过的定点为一个焦点,且短轴长为4.(1)、求椭圆 的标准方程;(2)、已知椭圆 的中心在原点,焦点在 轴上,且长轴和短轴的长分别是椭圆 的长轴和短轴的长的 倍 ,过点 的直线 与椭圆 交于 , 两个不同的点,若 ,求 的面积的最大值.