初中数学浙教版八年级上册第二章 特殊三角形 单元测试
试卷更新日期:2021-08-03 类型:单元试卷
一、单选题
-
1. 以下四个标志,每个标志都有图案和文字说明,其中的图案是轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知等腰三角形的两边长分别是 和 ,则周长为( )A、 B、 C、 或 D、3. 已知等腰三角形的一个内角等于 ,则该三角形的一个底角是( )A、 B、 或 C、 或 D、4. 命题“锐角小于90度”的逆命题是( )A、如果这个角是锐角,那么这个角小于90度 B、不是锐角的角不小于90度 C、不小于90度的角不是锐角 D、小于90度的角是锐角5. 如图所示的正方形网格中,网格线的交点为格点,已知A,B是两个定格点,如果C也是图中的格点,且使得 为等腰三角形,则点C的个数是( )
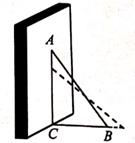
2. 已知等腰三角形的两边长分别是 和 ,则周长为( )A、 B、 C、 或 D、3. 已知等腰三角形的一个内角等于 ,则该三角形的一个底角是( )A、 B、 或 C、 或 D、4. 命题“锐角小于90度”的逆命题是( )A、如果这个角是锐角,那么这个角小于90度 B、不是锐角的角不小于90度 C、不小于90度的角不是锐角 D、小于90度的角是锐角5. 如图所示的正方形网格中,网格线的交点为格点,已知A,B是两个定格点,如果C也是图中的格点,且使得 为等腰三角形,则点C的个数是( ) A、6个 B、7个 C、8个 D、9个6. 如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
A、6个 B、7个 C、8个 D、9个6. 如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )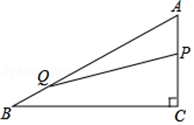 A、2s B、4s C、2s或4.5s D、2s或4s7. 如图,在 中, 的垂直平分线交 于 ,交 于 ,则 的长为( )
A、2s B、4s C、2s或4.5s D、2s或4s7. 如图,在 中, 的垂直平分线交 于 ,交 于 ,则 的长为( ) A、 B、 C、 D、8. 如图,一棵树从3m处折断了,树顶端离树底端距离4m,那么这棵树原来的高度是:( )
A、 B、 C、 D、8. 如图,一棵树从3m处折断了,树顶端离树底端距离4m,那么这棵树原来的高度是:( )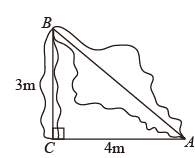 A、8m B、5m C、9m D、7m9. 以下列各组数为边长,可以构成直角三角形的是( )A、5,12,13 B、1,2,3 C、3,3,3 D、4,5,610. 如图,在 和 中, ,则下列说法错误的是( )
A、8m B、5m C、9m D、7m9. 以下列各组数为边长,可以构成直角三角形的是( )A、5,12,13 B、1,2,3 C、3,3,3 D、4,5,610. 如图,在 和 中, ,则下列说法错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
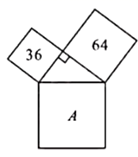
11. “等腰三角形的两个底角相等”的逆命题是.12. 如图,数字代表所在正方形的面积,则A所代表的正方形的面积为.
 13. 同一平面内有 , , 三点, , 两点之间的距离为 ,点 到直线 的距离为 ,且 为直角三角形,则满足上述条件的点 有个.14. 如图,点 在 内部, ,若添加一个条件: . 则 是等边三角形.
13. 同一平面内有 , , 三点, , 两点之间的距离为 ,点 到直线 的距离为 ,且 为直角三角形,则满足上述条件的点 有个.14. 如图,点 在 内部, ,若添加一个条件: . 则 是等边三角形. 15. 如图,在 中, , , ,若D是 边上的动点,则 的最小值为.
15. 如图,在 中, , , ,若D是 边上的动点,则 的最小值为. 16. 在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P、Q两点分别在边AC和射线AX上移动.当PQ=AB,AP=时,△ABC和△APQ全等.
16. 在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P、Q两点分别在边AC和射线AX上移动.当PQ=AB,AP=时,△ABC和△APQ全等.
三、解答题
-
17. 在 的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使整个阴影部分组成的图形成轴对称图形,请画出三种情形.
 18. 如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=125°.求∠ACB和∠BAC的度数.
18. 如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=125°.求∠ACB和∠BAC的度数. 19. 如图, 中, ,CD是 的高, , ,求BD长.
19. 如图, 中, ,CD是 的高, , ,求BD长.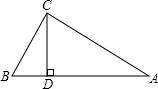 20. 在△ABC中,AB=AC,∠A=36°,CD平分∠ACB交AB于点D,DE⊥AC交AC于点E,若BD=7,且△BDC的周长为29,求AE的长.
20. 在△ABC中,AB=AC,∠A=36°,CD平分∠ACB交AB于点D,DE⊥AC交AC于点E,若BD=7,且△BDC的周长为29,求AE的长. 21. 如图,A , B , H是直线l上的三个点,AC⊥l于点A , BD⊥l于点B , 且HC=HD , AB=5,AC=2,BD=3,求AH的长.
21. 如图,A , B , H是直线l上的三个点,AC⊥l于点A , BD⊥l于点B , 且HC=HD , AB=5,AC=2,BD=3,求AH的长. 22. 已知:如图,点B,F,C,E在同一直线上, , 相交于点G, ,垂足为B, ,垂足为E,且 , .求证: .
22. 已知:如图,点B,F,C,E在同一直线上, , 相交于点G, ,垂足为B, ,垂足为E,且 , .求证: .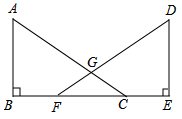
四、综合题