湖北省重点高中智学联盟2020-2021学年高二下学期数学期末联考试卷
试卷更新日期:2021-08-03 类型:期末考试
一、单选题
-
1. 下列与集合 相等的是( )A、 B、 C、 D、2. 若函数 的定义域为( )A、 ( ) B、 ( ) C、 ( ) D、 ( )3. 下列各函数中,值域为 的是( )A、 B、 C、 D、4. 若 为第三象限角,则( )A、 B、 C、 D、5. 下列选项中, 可表示为 的函数是( )A、 B、 C、 D、6. 已知 是数列 的前 项和,则“ ”是“数列 是公差为2的等差数列”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 集合 或 , ,若 ,则实数 的取值范围是( )A、 B、 C、 D、8. 若函数 在区间 上是单调函数,则实数 的取值范围是( )A、 B、 C、 D、
二、多选题
-
9. 已知函数 的导函数 的图象如图所示,则下列选项中正确的是( )
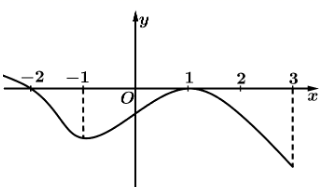 A、函数 在 处取得极小值 B、 是函数 的极值点 C、 在区间 上单调递减 D、 的图象在 处的切线斜率大于零10. 若集合 , 满足: , ,则下列关系可能成立的是( )A、 B、 C、 D、11. 先将曲线 上每个点的横坐标伸长为原来的2倍(纵坐标不变),再将图象向下平移 个单位,得到 的图象,则下列说法正确的是( )A、 B、 在 上的值域为 C、 的图象关于点 对称 D、 的图象可由 的图象向右平移 个单位长度得到12. 函数 是定义在 上的奇函数,当 时, ,则下列结论正确的是( )A、当 时, B、关于 的不等式 的解集为 C、关于 的方程 有三个实数解 D、 ,
A、函数 在 处取得极小值 B、 是函数 的极值点 C、 在区间 上单调递减 D、 的图象在 处的切线斜率大于零10. 若集合 , 满足: , ,则下列关系可能成立的是( )A、 B、 C、 D、11. 先将曲线 上每个点的横坐标伸长为原来的2倍(纵坐标不变),再将图象向下平移 个单位,得到 的图象,则下列说法正确的是( )A、 B、 在 上的值域为 C、 的图象关于点 对称 D、 的图象可由 的图象向右平移 个单位长度得到12. 函数 是定义在 上的奇函数,当 时, ,则下列结论正确的是( )A、当 时, B、关于 的不等式 的解集为 C、关于 的方程 有三个实数解 D、 ,三、填空题
-
13. 函数 为定义在 上的奇函数,且满足 ,若 ,则 .14. 请根据矩形图表信息,补齐不等式: .
 15. 若函数 在区间 只有一个极值点,则实数 的取值范围为.16. 法国著名的军事家拿破仑.波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”.在三角形 中,角 ,以 为边向外作三个等边三角形,其外接圆圆心依次为 ,若三角形 的面积为 ,则三角形 的周长最小值为
15. 若函数 在区间 只有一个极值点,则实数 的取值范围为.16. 法国著名的军事家拿破仑.波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”.在三角形 中,角 ,以 为边向外作三个等边三角形,其外接圆圆心依次为 ,若三角形 的面积为 ,则三角形 的周长最小值为四、解答题
-
17. 设全集为 ,不等式 的解集为 ,不等式 的解集为 .(1)、求 ;(2)、求 .18. 在① ,② ,③ 中任选一个条件,补充在下面问题中,并解决问题.
已知 ,_____, .
(1)、求 的值;(2)、求 .19. 已知函数 .(1)、求定义域及单调区间;(2)、求 的极值点.
