初中数学浙教版八年级上册第一章 三角形的初步知识 单元测试
试卷更新日期:2021-08-03 类型:单元试卷
一、单选题
-
1. 下列各组数中,不可能成为一个三角形的三边的长的一组数是( )A、5,6,7 B、5,7,13 C、5,8,8 D、5,12,132. 将一副三角板按如图方式重叠,则 的度数为( )
 A、 B、 C、 D、3. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A、
A、 B、 C、 D、3. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A、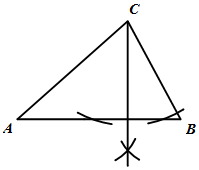 B、
B、 C、
C、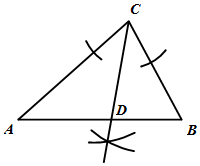 D、
D、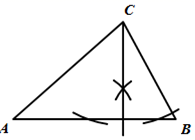 4. 如图 , , 其中 , , , , ,则到距离为( )
4. 如图 , , 其中 , , , , ,则到距离为( ) A、3 B、5 C、 D、5. 下列命题中的真命题是( )A、在所有连接两点的线中直线最短 B、经过两点有且只有一条直线 C、内错角互补则两直线平行 D、空间中,如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直6. 如图,∠A、∠1、∠2的大小关系是( )
A、3 B、5 C、 D、5. 下列命题中的真命题是( )A、在所有连接两点的线中直线最短 B、经过两点有且只有一条直线 C、内错角互补则两直线平行 D、空间中,如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直6. 如图,∠A、∠1、∠2的大小关系是( ) A、∠A>∠1>∠2 B、∠2>∠1>∠A C、∠A>∠2>∠1 D、∠2>∠A>∠17. 下列说法中:①过一点有且只有一条直线与已知直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③在同一平面内,不重合的两条直线的位置关系只有相交和平行两种;④不相交的两条直线叫作平行线,错误的个数是( )A、1个 B、2个 C、3个 D、4个8. 下列说法中正确的是( )A、两个面积相等的图形,一定是全等图形 B、两个等边三角形是全等图形 C、两个全等图形的面积一定相等 D、若两个图形周长相等,则它们一定是全等图形9. 如图, , , 于点E, 于点D, , ,则 的长是( )
A、∠A>∠1>∠2 B、∠2>∠1>∠A C、∠A>∠2>∠1 D、∠2>∠A>∠17. 下列说法中:①过一点有且只有一条直线与已知直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③在同一平面内,不重合的两条直线的位置关系只有相交和平行两种;④不相交的两条直线叫作平行线,错误的个数是( )A、1个 B、2个 C、3个 D、4个8. 下列说法中正确的是( )A、两个面积相等的图形,一定是全等图形 B、两个等边三角形是全等图形 C、两个全等图形的面积一定相等 D、若两个图形周长相等,则它们一定是全等图形9. 如图, , , 于点E, 于点D, , ,则 的长是( )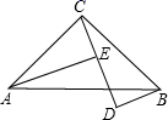 A、8 B、4 C、3 D、210. 如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B的距离,判定△EDC≌△ABC的依据是:( )
A、8 B、4 C、3 D、210. 如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B的距离,判定△EDC≌△ABC的依据是:( )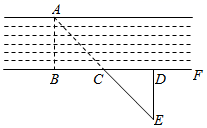 A、ASA B、SSS C、AAS D、SAS
A、ASA B、SSS C、AAS D、SAS二、填空题
-
11. 若长度分别为3,4,a的三条线段能组成一个三角形,则整数a的值可以是.(写出一个即可)12. 如图,∠EAD为锐角,C是射线AE上一点,点B在射线AD上运动(点A与点B不重合),设点C到AD的距离为d,BC长度为a,AC长度为b,在点B运动过程中,b、d保持不变,当a满足条件时,△ABC唯一确定.
 13. 如图,已知 ,若以“SAS”为依据证明 ,还要添加的条件 .
13. 如图,已知 ,若以“SAS”为依据证明 ,还要添加的条件 . 14. 如图,△ABD与△EBC全等,点A和点E是对应点,AB=1,BC=3,则DE的长等于 .
14. 如图,△ABD与△EBC全等,点A和点E是对应点,AB=1,BC=3,则DE的长等于 . 15. 如图,已知AB∥CD,∠A=65°,∠C=40°,则∠E的度数是
15. 如图,已知AB∥CD,∠A=65°,∠C=40°,则∠E的度数是 16. 已知三条不同的直线a,b,c在同一平面内,如果 , ,那么 ,这是一个命题.(填“真”或“假”)
16. 已知三条不同的直线a,b,c在同一平面内,如果 , ,那么 ,这是一个命题.(填“真”或“假”)三、解答题
-
17. 如图,每个小方格的边长都为1.求图中格点四边形ABCD的面积.
 18. 判断下列命题是真命题还是假命题,如果是假命题,请举出一个反例.(1)、如果一个数是偶数,那么这个数是4的倍数.(2)、两个负数的差一定是负数.19. 如图,∠BAP+∠APD=180° , ∠1=∠2.判定∠E与∠F是否相等,说明理由.
18. 判断下列命题是真命题还是假命题,如果是假命题,请举出一个反例.(1)、如果一个数是偶数,那么这个数是4的倍数.(2)、两个负数的差一定是负数.19. 如图,∠BAP+∠APD=180° , ∠1=∠2.判定∠E与∠F是否相等,说明理由. 20. 如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
20. 如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数. 21. 如图, ,AD是 内部一条射线,若 , 于点E, 于点F.求证: .
21. 如图, ,AD是 内部一条射线,若 , 于点E, 于点F.求证: . 22. 已知:如图,四边形 .
22. 已知:如图,四边形 .求作:点 ,使点 在四边形 内部, ,并且点 到 两边的距离相等.
 23. 如图,在Rt△ABC中,∠ACB=90°,且AC=AD .
23. 如图,在Rt△ABC中,∠ACB=90°,且AC=AD .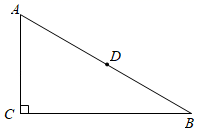 (1)、作∠BAC的平分线,交BC于点E;(要求尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接DE , 证明 .24.(1)、问题背景
(1)、作∠BAC的平分线,交BC于点E;(要求尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接DE , 证明 .24.(1)、问题背景如图1:在四边形ABCD中,AB=AD, BAD=120°, B= ADC=90°.E,F 分别是 BC,CD上的点.且 EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG.先证明ΔABE≌ΔADG;再证明ΔAEF≌ΔAGF,可得出结论,他的结论应是 ;
请你帮他完成证明过程
 (2)、探索延伸:
(2)、探索延伸:如图2,若在四边形ABCD中,AB=AD, B+ D=180°.E,F分别是BC,CD上的点,且 EAF= BAD,上述结论是否仍然成立,并说明理由;
(3)、实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(0处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲,乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.