贵州省遵义市2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 实数﹣ $\frac{1}{2}$ 的相反数是（）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 4 的平方根是（）

A、2 B、-2 C、±2 D、±4

查看试题解析
3. 受疫情影响，2020年第一季度遵义经济出现逆势增长，第一季度地区生产总值约为791亿元，按可比价计算，比上年同期增长0.8%.将791亿这个数用科学记数法表示为（）

A、791×10⁸ B、79.1×10⁹ C、7.91×10¹⁰ D、7.91×10¹¹

查看试题解析
4. 下列运算正确的是（　　）

A、（﹣1）²⁰²⁰＝﹣1 B、﹣2²＝4 C、 $\sqrt{16}$ ＝±4 D、 $\sqrt[3]{- 27}$ ＝﹣3

查看试题解析
5. 如图，直线 $a ∥ b$ ，三角板的直角顶点放在直线 $b$ 上，两直角边与直线 $a$ 相交，如果 $∠ 1 = 60 °$ ，那么 $∠ 2$ 等于（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
6. 若 $\{\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 是关于x、y的二元一次方程ax-3y=1的解，则a的值为（）

A、-5 B、-1 C、2 D、7

查看试题解析
7. 不等式组 ${\begin{array}{l} x - 1 > 0 \\ x - 2 ⩽ 0 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
8. 足球运动是全球体育界最具响力的单项体育场动，故有世界第一大运动的美称，为了解某学校校园足球与学生数占学校总人数的百分比，最合适的统计方式是（）

A、折线统计图 B、条形统计图 C、扇形统计图 D、直方图

查看试题解析
9. 下列命中，真命题是（）

A、相等的两个角是对顶角 B、如果两条直线被第三条直线所截，那么同位角相等 C、从直线外一点到这条直线的垂线段叫做该点到直线的距离 D、在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
10. 如果a＞b，那么下列不等式成立的是（）

A、﹣2a＞﹣2b B、 $\frac{a}{2} > \frac{b}{2}$ C、a+2＜b+2 D、a﹣2＜b﹣2

查看试题解析
11. 如图，将长方形纸条ABCD沿EF折叠后，ED与BF交于G点，若∠EFC＝130°，则∠AED的度数为（）

A、55° B、70° C、75° D、80°

查看试题解析
12. 我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（）

A、 ${\begin{array}{l} x + y = 100 \\ 3 x + 3 y = 100 \end{array}$ B、 ${\begin{array}{l} x + y = 100 \\ x + \frac{1}{3} y = 100 \end{array}$ C、 ${\begin{array}{l} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{array}$ D、 ${\begin{array}{l} x + y = 100 \\ 3 x + y = 100 \end{array}$

查看试题解析

二、填空题

13. 比较大小： $\sqrt[3]{9}$ 2.5

查看试题解析
14. 已知关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - y = k + 2 \\ x - 2 y = - k + 3 \end{array}$ ，则x﹣y的值是.

查看试题解析
15. 已知不等式组 ${\begin{array}{l} x - 2 < 3 - x \\ 2 (x - 1) > x - 1 \end{array}$ ，x是非负整数，则x的值是．

查看试题解析
16. 如图，将 $△$ ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A₁处，称为第1次操作，折痕DE到BC的距离记为h₁ ，还原纸片后，再将 $△$ ADE沿着过AD中点D₁的直线折叠，使点A落在DE边上的A₂处，称为第2次操作，折痕D₁E₁到BC的距离记为h₂ ，按上述方法不断操作下去…经过第2020次操作后得到的折痕D₂₀₂₀E₂₀₂₀到BC的距离记为h₂₀₂₀ ，若h₁＝1，则h₂₀₂₀的值为.

查看试题解析

三、解答题

17.

(1)、计算： $| 1 - \sqrt{2} | + \sqrt[3]{8} - \sqrt{2}$ ；

(2)、解方程： ${\begin{array}{l} y = 2 x - 3 \\ 3 x + 2 y = 8 \end{array}$ .

查看试题解析
18. 解不等式 $\frac{x + 3}{5} ⩽ \frac{2 x - 5}{3} - 1$ ，并把解集在数轴上表示出来.

查看试题解析
19. 先化简，再求值 $2 (- 3 x^{2} y + 4 x y^{2}) - 4 (\frac{1}{2} x y^{2} - \frac{3}{2} x^{2} y + 2)$ ，其中x＝﹣1，y＝ $\sqrt{2}$ .

查看试题解析
20. 如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG相交于点H，∠C＝∠EFG，∠BFG＝∠AEM，求证：AB∥CD.（完成下列填空）
证明：∵∠BFG＝∠AEM（已知）

且∠AEM＝∠BEC（   ）

∴∠BEC＝∠BFG（等量代换）

∴MC∥▲ （   ）

∴∠C＝∠FGD（   ）

∵∠C＝∠EFG（已知）

∴∠▲ ＝∠EFG，（等量代换）

∴AB∥CD（   ）

查看试题解析
21. 为了加强学生的交通安全意识，遵义交利用微信公众号发布了交通安全知识在线测试从中抽取了部分学生在线测试成绩（分数取正整数，满分为100分）进行统计，绘制了下面不完整的频数分布直方图和扇形统计图，根据图中提供的信息解答下列问题：

(1)、求样本容量和a的值；

(2)、求D等级对应扇形圆心角的度数；

(3)、补全频数分布直方图；

(4)、若交通安全知识在线测试成绩在80分以上为优秀，某学校共有1800名学生，估计该校成绩优秀的学生约为多少名？

查看试题解析
22. 如图，方格纸上每个小正方形的边长均为1个单位长度，点A，B，C都在格点上（两条网格线的交点叫格点）.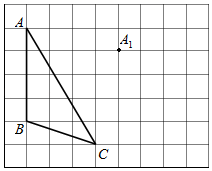

(1)、①平移 $△$ ABC，使点A移动到点A₁ ，请在网格纸上画出平移后的 $△$ A₁B₁C₁；
②作 $△$ ABC的高CE；

(2)、在（1）的条件下，求平移过程中，线段AB扫过的面积.

查看试题解析

23. 受新冠疫情扩散的影响，市场上防护口罩出现热销，某药店购进一批A、B两种不同型号的口罩进行销售.如表是甲、乙两人购买A.B两种型号口罩的情况：

	A型口罩数量（个）	B型口罩数量（个）	总售价（元）
甲	1	3	26
乙	3	2	29

(1)、求一个A型口罩和一个B型口罩的售价各是多少元？

(2)、某同学准备用不超过300元的资金购买两种型号的口罩，其中A型口罩数比B型口罩的3倍还要多5个，则A型口罩最多购买多少个？

查看试题解析

24. 如图

(1)、[问题解决]如图1，AB∥CD，点E、F分别是AB、CD上的点，连接OE、OF，探求∠1、∠2、∠3之间的关系，并说明理由.

(2)、[拓展延伸]如图2，上述结论还成立吗？如果成立，请证明；如果不成立，请写出它们的关系.

(3)、 [拓展应用]如图3，已知AB∥CD，∠AE₁E₂的角平分线与∠CE_nE_n_﹣1的角平分线交于点O.若∠E₁OE_n＝m°直接写出∠2+∠3+∠4+…+∠（n﹣2）+∠（n﹣1）的度数.（用含m、n的代数式表示）

查看试题解析