贵州省铜仁市德江县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. ${(x^{2})}^{4}$ 等于（）

A、 $x^{6}$ B、 $x^{8}$ C、 $x^{16}$ D、 $2 x^{4}$

查看试题解析
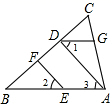
2. 下列等式从左到右的变形，属于因式分解的是（）

A、 $a (x - y) = a x - a y$ B、 $x^{3} - x = x (x + 1) (x - 1)$ C、 $(x + 1) (x + 3) = x^{2} + 4 x + 3$ D、 $x^{2} + 2 x + 1 = x (x + 2) + 1$

查看试题解析
3. 如图，直线a，b，c，d，已知c⊥a，c⊥b，直线b，c，d交于一点，若∠1=48°，则∠2等于（）

A、42° B、48° C、40° D、45°

查看试题解析
4. 方程 $3 x + 5 y = 29$ 与下列（）方程所组成的方程组的解是 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$

A、 $4 x + 6 y = - 6$ B、 $4 x + 7 y = 40$ C、 $2 x - 3 y = 13$ D、以上答案都不对

查看试题解析
5. 图（1）是一个长为 $2 a$ ，宽为 $2 b$ （ $a$ ＞ $b$ ）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（）．

A、 $2 a b$ B、 ${(a + b)}^{2}$ C、 ${(a - b)}^{2}$ D、 $a^{2} - b^{2}$

查看试题解析
6. 甲乙两位初三学生练习1000米跑步，如果乙先跑20米，则甲10秒钟可以追上乙，如果乙先跑2秒钟，则甲4秒钟可以追上乙，求甲、乙两人每秒钟各跑多少米.若设甲每秒钟跑x米，乙每秒钟跑y米，则所列方程组应该是（）

A、 ${\begin{array}{l} 20 = 10 (x - y) \\ (2 + 4) y = 4 x \end{array}$ B、 ${\begin{array}{l} 10 x - 10 y = 20 \\ 4 x - 4 y = 4 \end{array}$ C、 ${\begin{array}{l} 10 x + 20 = 10 y \\ 4 x - 4 y = 2 \end{array}$ D、 ${\begin{array}{l} 10 x = 10 y + 20 \\ 4 x - 2 = 4 y \end{array}$

查看试题解析
7. 下列各式中，与 $(1 - b) (- b - 1)$ 相等的是（）

A、 $b^{2} - 1$ B、 $b^{2} - 2 b + 1$ C、 $b^{2} - 2 b - 1$ D、 $b^{2} + 1$

查看试题解析
8. 若 $x^{2} + k x + 49$ 是一个完全平方式，则k的值是（）

A、14 B、7 C、±14 D、±7

查看试题解析
9. 已知 $(x^{2} + a x) (x^{2} - 3 x + b)$ 的乘积中不含 $x^{2}$ 项和 $x^{3}$ 项，则a，b的值为（）

A、 $a = 0 ， b = 0$ B、 $a = 3 ， b = 9$ C、 $a = - 3 ， b = 9$ D、 $a = 3 ， b = - 9$

查看试题解析
10. “深池一芦苇，出头六分一，若水涨五寸，出头仅一分，水下十一分，水苇各几多？”通过上面的描述，求得水深与芦苇长各为（）

A、50寸，60寸 B、60寸，50寸 C、50寸，40寸 D、40寸，50寸

查看试题解析

二、填空题

11. 计算： $3 x \cdot x^{2} + x^{3}$ .

查看试题解析
12. 方程组 ${\begin{array}{l} x + y = 4 \\ 2 x - y = 2 \end{array}$ 的解是．

查看试题解析
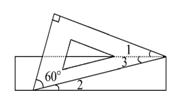
13. 已知 $a^{x} = 2$ ， $a^{y} = - 3$ ，求 $a^{x + 2 y} =$ .

查看试题解析
14. 如图，有一块含有60°角的直角三角板的两个顶点放在长方形的对边上.如果∠1=17°，那么∠2的度数是.

查看试题解析
15. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
16. 有大小两种笔记本，3本大笔记本和2本小笔记本的售价是14元，2本大笔记本和3本小笔记本的售价为11元.设大笔记本为x元/本，小笔记本为y元/本，根据题意，列方程组正确的是.

查看试题解析
17. 多项式4x²+1加上一个单项式，使它成为一个整式的完全平方，则这个单项式可以是 .（填写符合条件的一个即可）

查看试题解析
18. 若 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ 是方程组 ${\begin{array}{l} 4 x - 7 y = a + b \\ 2 x - y = a - b \end{array}$ 的解，则 $a ， b$ 的值分别是.

查看试题解析

三、解答题

19. 计算： ${(- 2 a^{2} b)}^{^{3}} • 3 {(a b^{2})}^{2}$ .

查看试题解析
20. 先化简，再求值： ${(x + 3)}^{2} + (x + 2) (x - 2) - 2 x^{2}$ ，其中 $x = - \frac{1}{3}$ .

查看试题解析
21. 已知 $x + y = 2$ ， $x y = - 3$ ，求 $2 {(x y)}^{2} + x^{3} y + x y^{3}$ 的值.

查看试题解析
22. 在日常生活中，如取款、上网需要密码，有一种因式分解法产生密码，例如 $x^{4} - y^{4} = (x - y) (x + y) (x^{2} + y^{2})$ ，当 $x = 9 ， y = 9$ 时， $x - y = 0$ ， $x + y = 18$ ， $x^{2} + y^{2} = 162$ ，则密码018162或180162等.对于多项式 $4 x^{3} - x y^{2}$ ，取 $x = 10 ， y = 10$ ，用上述方法产生密码是什么？

查看试题解析
23. 为了加快脱贫致富的步伐，某村返乡农民工在攻坚队的帮扶下成立了养殖合作社，第一批购进15头大牛和5头小牛，每天用饲料325kg；一个月后，该合作社决定扩大养殖规模，又购进了10头大牛和5头小牛，这时每天所用饲料比原来多225kg.问每头大牛和每头小牛每天各需多少饲料？

查看试题解析
24. 如图，已知EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD（请填空）

解：∵EF∥AD，

∴∠2=▲ （   ）.

又∵∠1=∠2（   ），

∴∠1=∠3（   ），

∴AB∥▲ （   ），

∴∠BAC+▲ =180°（   ）.

∵∠BAC=70°（   ），

∴∠AGD=（   ）.

查看试题解析