贵州省六盘水市2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中，属于轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 $a^{6} \div a^{2} = a^{3}$ B、 $a \div a^{4} = a^{5}$ C、 ${(a b^{3})}^{2} = a^{2} b^{6}$ D、 $a - (3 b - a) = - 3 b$

查看试题解析
3. 如图，将一块含有 $45^{\circ}$ 角的直角三角板的两个顶点放在一把直尺的对边上，如果 $∠ 1 = 25^{\circ}$ ，那么 $∠ 2$ 的度数是（）

A、30° B、25° C、20° D、15°

查看试题解析
4. 下列成语所描述的事件，是随机事件的是（）

A、水涨船高 B、一箭双雕 C、水中捞月 D、一步登天

查看试题解析
5. 如图， $∠ A D C = ∠ A D B$ ，添加一个条件，仍不能说明 $△ A B D ≌ △ A C D$ 的是（）

A、 $A B = A C$ B、 $∠ B A D = ∠ C A D$ C、 $∠ B = ∠ C$ D、 $B D = C D$

查看试题解析
6. 若 $a = π^{0}$ ， $b = 2^{- 2}$ ， $c = {(- 2)}^{2}$ ，则下列式子正确的是（）

A、 $a < b < c$ B、 $c < b < a$ C、 $b < a < c$ D、 $a < c < b$

查看试题解析
7. 清晨，驾驶员小张要驾驶汽车去公司上班，发动汽车后预热（发动汽车后在原地稍作等待）了几秒，然后开始加速行驶，突然发现前面不远处有障碍物，于是便紧急刹车停了下来.下面几幅图中，能更好的刻画小张从发动汽车到停车这一行车过程中速度与时间之间关系的是（）

A、 B、 C、 D、

查看试题解析
8. 用三角板作 $△ A B C$ 的边BC上的高，下列三角板的摆放位置正确的是（）

A、 B、 C、 D、

查看试题解析
9. 已知一个角的补角比它的余角的3倍小20度，则这个角的度数是（）

A、 $30^{\circ}$ B、 $35 °$ C、 $40^{\circ}$ D、 $45^{\circ}$

查看试题解析
10. 如图，在 $△ A B C$ 中，点D在边BC上，点 $E ， F$ 分别是 $A D ， C E$ 的中点，且 $△ B E F$ 的面积为3，则 $△ A B C$ 的面积是（）

A、9 B、10 C、11 D、12

查看试题解析

二、填空题

11. “飞沫传播”是新冠肺炎病毒传播的一种途径，小明查阅相关资料，发现“飞沫”的直径一般在0.000003米左右，佩戴“N95”口罩能有效的把“飞沫”吸附住，将0.000003米用科学记数法表示为米.

查看试题解析

12. 一抹“凉都绿”，一杯生态茶.凉都茶叶因其得天独厚的生长条件，具有早采、富硒、有机的天然品质，凉都具备发展优质茶产业的先天地理优势，茶产业已成为六盘水农业特色产业之一，下表是我市某茶叶种植合作社脱贫攻坚期间茶树种植成活情况统计表：

种植茶树棵树	3000	5000	8000	10000	20000	$\dots$
成活棵树	2690	4507	7195	9003	17998	$\dots$
成活率	0.8967	0.9014	0.8993	0.9003	0.8999	$\dots$

根据这个表格，请估计这个合作社茶树种植成活的概率为（结果保留一位小数）

查看试题解析

13. 如图所示，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 40^{°}$ ，AB的垂直平分线交AB于点D ，交AC于点E ，连接BE ，则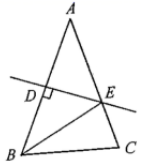 $∠ C B E$ 的度数为（）

查看试题解析
14. 如图所示是一种计算程序，若开始输入的值为2，则最后输出的结果是.

查看试题解析
15. 动手操作是学习数学的一种好方法，如图，小华同学在一次折纸活动中，将一张 $A_{4}$ 纸（ $A_{4}$ 纸是一张长 $A B = 29.7 c m$ ，宽 $B C = 21 c m$ 的长方形纸片）沿AE折叠，使点B落在CD边上的点F处，如果 $△ A D F$ 的周长为 $71.7 c m$ ，则 $△ F C E$ 的周长为 $c m$ .

查看试题解析

三、解答题

16. 运用整式乘法公式进行计算： $2018 \times 2022 - 2020^{2}$

查看试题解析
17. 先化简，再求值： $[{(x + 2 y)}^{2} - {(x - 2 y)}^{2}] \div 4 x$ ，其中 $x = 2$ ， $y = - 1$ .

查看试题解析
18. 如图，直线 $a ， b$ 被直线 $m ， n$ 所截，若 $∠ 1 + ∠ 2 = 180^{\circ}$ ， $∠ 3 = 58^{\circ}$ ，求 $∠ 4$ 的度数.

查看试题解析
19. 某单位在创建全国文明城市志愿者服务活动中，需要一名学生志愿者，小明和小丽都想参加.聪明的小华为他们设计了一个游戏：在一个不透明的口袋中放入5个黑球和3个白球，每个球的形状和大小都相同，充分摇匀后，小华随机摸出一个球，如果是黑球，则小明去；如果是白球，则小丽去.

(1)、这个游戏对小明和小丽公平吗？请说明理由.

(2)、如果游戏不公平，怎样修改游戏才能使游戏公平？

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ A B C = 110^{\circ}$ ， $∠ A = 40^{\circ}$ .

(1)、作 $△ A B C$ 的角平分线BE（点E在AC上；用尺规作图，不写作法，保留作图痕迹）；

(2)、在（1）的条件下，求 $∠ B E C$ 的度数.

查看试题解析
21. 为弘扬中华优秀传统文化，我市某中学决定根据学生的兴趣爱好组建课外兴趣小组，因此，学校随机调查了部分同学的兴趣爱好，将收集的数据整理并绘制成下列两幅不完整的统计图，请根据图中的信息，完成下列问题：

(1)、学校这次调查共抽取了名学生；

(2)、补全条形统计图；

(3)、在扇形统计图中，“诗词”所在扇形的圆心角度数为度；

(4)、该校有150名学生喜欢“戏曲”.学生1500名，请你估计该校有多少名学生喜欢“戏曲”？

查看试题解析

22. 2019年，果农小林家的刺梨喜获丰收.在销售过程中，刺梨的销售额y（元）与销量x（千克）满足如下关系：

销量 $x$ （千克）	1	2	3	4	5	6	7	8
销售额 $y$ （元）	3	6	9	12	15	18	21	24

(1)、上表这个变化过程中，自变量是，因变量是；

(2)、刺梨的销售额

y

（元）与销量

x

（千克）之间的关系式为；

(3)、当刺梨销量为50千克时，销售额是多少元？

查看试题解析

23. 如图，点 $E ， F$ 分别是线段 $A D$ 上的两点， $A E = D F$ ， $A B / / C D$ ， $A B = C D$ ，线段 $C E$ 与 $B F$ 有什么数量关系和位置关系？请说明理由.

查看试题解析
24. 先仔细阅读材料，再尝试解决问题：通过上学期对有理数的乘方的学习，我们知道 $x^{2} \geq 0$ ，本学期学习了完全平方公式后，我们知道 $a^{2} \pm 2 a b + b^{2} = {(a \pm b)}^{2}$ ，所以 ${(a \pm b)}^{2} \geq 0$ ，这一性质在数学中有着广泛的应用，比如，探究多项式 $2 x^{2} + 4 x - 5$ 的最小值时，我们可以这样处理：
解：原式 $= 2 (x^{2} + 2 x) - 5$

$= 2 (x^{2} + 2 x + 1^{2} - 1^{2}) - 5$

$= 2 [{(x + 1)}^{2} - 1^{2}] - 5$

$= 2 {(x + 1)}^{2} - 2 - 5$

$= 2 {(x + 1)}^{2} - 7$

因为 ${(x + 1)}^{2} ⩾ 0$ ，所以 $2 {(x + 1)}^{2} - 7 ⩾ 0 - 7$ ，即 $2 {(x + 1)}^{2} - 7 \geq - 7$

所以 $2 {(x + 1)}^{2} - 7$ 的最小值是 $- 7$ ，即 $2 x^{2} + 4 x - 5$ 的最小值是 $- 7$

请根据上面的探究思路，解答下列问题：

(1)、多项式 $5 {(x - 3)}^{2} + 1$ 的最小值是；

(2)、求多项式 $4 x^{2} - 16 x + 3$ 的最小值；

(3)、求多项式 $x^{2} + 6 x + y^{2} - 4 y + 20$ 的最小值.

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C = 3$ ， $∠ B = ∠ C = 50^{\circ}$ ，点D在边BC上运动（点D不与点 $B ， C$ 重合），连接AD，作 $∠ A D E = 50^{\circ}$ ，DE交边AC于点E.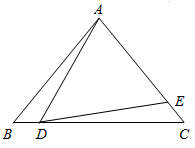

(1)、当 $∠ B D A = 100^{\circ}$ 时， $∠ E D C =$ $^{\circ}$ ， $∠ D E C =$ $^{\circ}$

(2)、当DC等于多少时， $△ A B D ≌ △ D C E$ ，请说明理由；

(3)、在点D的运动过程中， $△ A D E$ 的形状可以是等腰三角形吗？若可以，请求出 $∠ B D A$ 的度数；若不可以，请说明理由.

查看试题解析