甘肃省兰州市教育局第四片区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 下列艺术字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
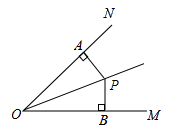
D、 2. 下列事件中,是必然事件的是( )A、经过有交通信号灯的路口,遇到红灯 B、明天太阳从西方升起 C、三角形内角和是 D、购买一张彩票,中奖3. 据科学检测,新冠病毒实际直径约为0.000011厘米,其中数据0.000011用科学记数法可以表示为( )A、 B、 C、 D、4. 已知等腰三角形顶角的度数是30°,则底角的度数为( )A、60° B、65° C、70° D、75°5. 如图, 平分 , , ,垂足分别为 、 ,若 ,则 ( )
2. 下列事件中,是必然事件的是( )A、经过有交通信号灯的路口,遇到红灯 B、明天太阳从西方升起 C、三角形内角和是 D、购买一张彩票,中奖3. 据科学检测,新冠病毒实际直径约为0.000011厘米,其中数据0.000011用科学记数法可以表示为( )A、 B、 C、 D、4. 已知等腰三角形顶角的度数是30°,则底角的度数为( )A、60° B、65° C、70° D、75°5. 如图, 平分 , , ,垂足分别为 、 ,若 ,则 ( )
 A、 B、 C、 D、6. 以下列各组线段为边,能组成三角形的是( )A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,直线AB∥CD,∠3=70°,则∠1=( )
A、 B、 C、 D、6. 以下列各组线段为边,能组成三角形的是( )A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,直线AB∥CD,∠3=70°,则∠1=( )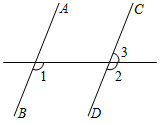 A、70° B、100° C、110° D、120°9. 重庆八中的老师工作很忙,但初一年级很多数学老师仍然坚持锻炼身体,比如张老师就经常坚持饭后走一走.某天晚饭后他从学校慢步到附近的中央公园,在公园里休息了一会后,因学校有事,快步赶回学校.下面能反映当天张老师离学校的距离y与时间x的关系的大致图象是( )A、
A、70° B、100° C、110° D、120°9. 重庆八中的老师工作很忙,但初一年级很多数学老师仍然坚持锻炼身体,比如张老师就经常坚持饭后走一走.某天晚饭后他从学校慢步到附近的中央公园,在公园里休息了一会后,因学校有事,快步赶回学校.下面能反映当天张老师离学校的距离y与时间x的关系的大致图象是( )A、 B、
B、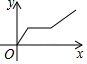 C、
C、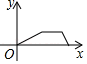 D、
D、 10. 如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( )
10. 如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( ) A、(m﹣n)2=m2﹣2mn+n2 B、(m+n)2=m2+2mn+n2 C、(m﹣n)2=m2+n2 D、m2﹣n2=(m+n)(m﹣n)11. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )
A、(m﹣n)2=m2﹣2mn+n2 B、(m+n)2=m2+2mn+n2 C、(m﹣n)2=m2+n2 D、m2﹣n2=(m+n)(m﹣n)11. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )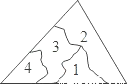 A、1;SAS B、2;ASA C、3;ASA D、4;SAS12. 如图,在 中, , 的平分线 交 于点 ,如果 垂直平分 ,那么 的度数为( )
A、1;SAS B、2;ASA C、3;ASA D、4;SAS12. 如图,在 中, , 的平分线 交 于点 ,如果 垂直平分 ,那么 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
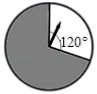
13. 已知 ,则 的余角的度数为.14. 如图,转动的转盘停止转动后,指针指向白色区域的概率是.
 15. 计算 .16. 如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为 三角形ACE的面积为y,则y与x的关系式为.
15. 计算 .16. 如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为 三角形ACE的面积为y,则y与x的关系式为.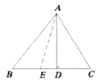
三、解答题
-
17. 计算(1)、 ;(2)、 ;(3)、 ;(4)、 .18. 利用整式乘法公式计算(1)、 ;(2)、 .19. 先化简,再求值:
,其中 , .
20. 如图, , , ,求证: . 21. 如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
21. 如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)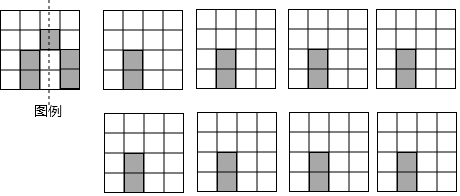 22. 某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券,(转盘被等分成20个扇形),已知甲顾客购物220元.
22. 某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券,(转盘被等分成20个扇形),已知甲顾客购物220元. (1)、他获得购物券的概率是多少?(2)、他得到100元、50元、20元购物券的概率分别是多少?(3)、若要让获得20元购物券的概率变为 ,则转盘的颜色部分怎样修改?(直接写出修改方案即可).23. 李老师周末骑自行车去郊游,如图是他离家的距离 (千米)与时间 (时)之间关系的函数图象,李老师9时离开家,15时到家,根据这个函数图象,请你回答下列问题:
(1)、他获得购物券的概率是多少?(2)、他得到100元、50元、20元购物券的概率分别是多少?(3)、若要让获得20元购物券的概率变为 ,则转盘的颜色部分怎样修改?(直接写出修改方案即可).23. 李老师周末骑自行车去郊游,如图是他离家的距离 (千米)与时间 (时)之间关系的函数图象,李老师9时离开家,15时到家,根据这个函数图象,请你回答下列问题: (1)、到达离家最远的地方是时,离家千米.(2)、他时开始了第二次休息,在整个骑行过程中,一共休息了小时.(3)、他从离家最远的地方回家用了多长时间?速度是多少?24. 如图所示,在一个边长为 的正方形的四个角都剪去一个大小相等的白色小正方形,当白色小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)、到达离家最远的地方是时,离家千米.(2)、他时开始了第二次休息,在整个骑行过程中,一共休息了小时.(3)、他从离家最远的地方回家用了多长时间?速度是多少?24. 如图所示,在一个边长为 的正方形的四个角都剪去一个大小相等的白色小正方形,当白色小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化. (1)、在这个变化过程中,是自变量,是因变量;(2)、如果小正方形的边长为 ,图中阴影部分的面积 ,请写出 与 的关系式;(3)、当小正方形的边长由 变化到 时,阴影部分的面积是怎样变化的?
(1)、在这个变化过程中,是自变量,是因变量;(2)、如果小正方形的边长为 ,图中阴影部分的面积 ,请写出 与 的关系式;(3)、当小正方形的边长由 变化到 时,阴影部分的面积是怎样变化的?(请算出阴影部分的面积具体变化的数值,并指出面积在增大还是减小)
25. 如图,在 中, , 是 中点, ,垂足为 .若 ,求 的度数.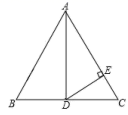 26. 看图填空,并在括号内注明说理依据.
26. 看图填空,并在括号内注明说理依据.如图,已知 , , , , 与 平行吗? 与 平行吗?
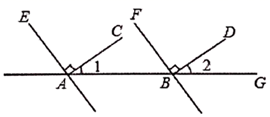
解:因为 , (已知),
所以 .
所以▲ ▲ ( ).
又因为 (已知),
所以 .( )
所以 .
同理可得, ▲ .
所以 ( ).
所以▲ ▲ (同位角相等,两直线平行).

