山西省吕梁市孝义市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 代数式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 2021年4月23日是第26个世界读书日.为迎接第26个世界读书日的到来,某校举办读书分享大赛活动,最终有13名同学进入决赛(他们决赛的成绩各不相同),比赛将评出一等奖1名,二等奖2名,三等奖3名.某参赛同学知道自己的分数后,要判断自己能否获奖,他需要知道这13名学生成绩的( )A、中位数 B、平均数 C、众数 D、方差3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,已知四边形 是平行四边形,对角线 与 相交于点 .添加下列条件仍不能判定 是菱形的是( )
 A、 B、 C、 D、5. 如图是某地区一天的气温随时间变化的图象,根据图象信息,下列说法正确的是( )
A、 B、 C、 D、5. 如图是某地区一天的气温随时间变化的图象,根据图象信息,下列说法正确的是( ) A、气温 (℃)不是时间 (时)的函数 B、这一天最高气温是14℃ C、4时至14时气温 (℃)随时间 (时)的增大而增大 D、24时气温最低6. 为了了解某种小麦的长势,随机抽取了50株麦苗进行测量,测量结果如下表:
A、气温 (℃)不是时间 (时)的函数 B、这一天最高气温是14℃ C、4时至14时气温 (℃)随时间 (时)的增大而增大 D、24时气温最低6. 为了了解某种小麦的长势,随机抽取了50株麦苗进行测量,测量结果如下表:苗高
10
11
12
13
14
株数(株)
7
12
10
14
7
则麦苗高的中位数和众数分别是( )
A、10,11 B、11,12 C、12,13 D、13,147. 根据勾股定理,任意直角三角形的两条直角边长 , ,和斜边长 都是含三个未知数的方程 的一组解,而每一组勾股数(例如3,4,5;5,12,13;等)都是这个方程的正整数解.高于二次的方程 , , ,…是否也有正整数解呢?法国数学家费马经过研究得出结论:当自然数 时,方程 没有正整数解.这个命题的证明引起了世界各国数学家的关注,最终由英国数学家怀尔斯于1995年完成了证明.困扰了数学家300多年历史的数学难题终于得到解决,在解决这一数学难题的过程中,反映了一代代数学家艰苦探索、不屈不挠的科学精神和聪明慧.这个定理的证明被称为“世纪性的成就”.这个定理指的是( )A、费马大定理 B、怀尔斯大定理 C、勾股定理 D、勾股定理的逆定理8. 如图, 中, , , , 是 边上的中线,则 的长度为( )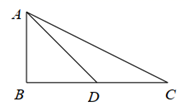 A、1 B、2 C、 D、9. 如图, 中,对角线 , 交于点 ,点 是 的中点,若 的周长是10, ,则 的长度为( )
A、1 B、2 C、 D、9. 如图, 中,对角线 , 交于点 ,点 是 的中点,若 的周长是10, ,则 的长度为( ) A、4 B、3 C、2 D、110. 同一平面直角坐标系中,一次函数 与 ( , 为常数)的图象可能是( )A、
A、4 B、3 C、2 D、110. 同一平面直角坐标系中,一次函数 与 ( , 为常数)的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 比较大小: 1(填“<”或“=”或“>”).12. 甲、乙两名同学分别进行6次射击训练,训练成绩及平均成绩方差如下表:(单位:环)
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
方差
甲
9
8
6
7
8
10
8
1.67
乙
8
7
8
9
9
7
8
0.67
甲和乙的训练成绩比较稳定的是 .
13. 如图,某港口 位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,“远航”号以每小时 的速度沿北偏东30°方向航行,“海天”号以每小时 的速度沿北偏西60°方向航行.一小时后,“远航”号、“海天”号分别位于 , 处,则此时“远航”号与“海天”号的距离为 . 14. 如图,一次函数 的图象与 轴交于点 ,与 轴交于点 ,与正比例函数 的图象交于点 ,且点 的横坐标为2,则不等式 的解集为 .
14. 如图,一次函数 的图象与 轴交于点 ,与 轴交于点 ,与正比例函数 的图象交于点 ,且点 的横坐标为2,则不等式 的解集为 . 15. 如图,正方形 中,点 是 边上一点, ,且 交正方形外角的平分线 于点 ,连接 .若 , ,则 的长为 .
15. 如图,正方形 中,点 是 边上一点, ,且 交正方形外角的平分线 于点 ,连接 .若 , ,则 的长为 .
三、解答题
-
16. 计算(1)、(2)、17. 文明其精神,野蛮其体魄.体育课上张老师对全班学生进行了体能测试,从跑步、立定跳远、跳绳三个方面进行了量化考核.小字和小彬的各项成绩如下表(百分制):
姓名
跑步
立定跳远
跳绳
小宇
85
95
90
小彬
95
86
88
若跑步、立定跳远、跳绳的成绩按 确定体能综合成绩,则小宇和小彬谁的体能综合成绩高?请通过计算说明理由.
18. 如图1是某学校的篮球架实物图,其侧面示意图如图2所示,“综合与实践”小组开展了测量篮板 长度的实践活动.在不便于直接测量的情况下,“综合与实践”小组设计了如下方案:课题
测量篮板的长度
成员
组长:xxx 组员:xxx , xxx , xxx
工具
竹竿,皮尺,计算器等
测量
示意图

说明: 垂直于地面于点 ,线段 , 表示同一根竹竿,第一次将竹竿的一个端点与点 重合,另一端点落在地面的点 处,第二次将竹竿的一个端点与点 重合,另一端点落在地面的点 处.
测量数据
测量项目
数值
竹竿的长度
5米
的长度
3.062米
的长度
4.073米
参考数值
, , ,
根据以上测量结果,请你帮助该“综合与实践”小组求出学校篮板 的长度(结果精确到0.01米).
 19. 新型冠状病毒的传染性非常强.“戴口罩,勤洗手,多通风”是必要的防护措施.新冠疫情以来,各学校都新增了洗手设备,我市某学校的洗手房一角,水龙头上面的墙壁上还张贴了“七步洗手法”的标语.在洗手的过程中,经常有学生关闭不严水龙头造成滴水,为了增强学生的节水意识,数学兴趣小组进行了漏水量与漏水时间的关系调查研究,在滴水的水龙头下放置一个量筒,每5分钟记录一次水量,如下表.
19. 新型冠状病毒的传染性非常强.“戴口罩,勤洗手,多通风”是必要的防护措施.新冠疫情以来,各学校都新增了洗手设备,我市某学校的洗手房一角,水龙头上面的墙壁上还张贴了“七步洗手法”的标语.在洗手的过程中,经常有学生关闭不严水龙头造成滴水,为了增强学生的节水意识,数学兴趣小组进行了漏水量与漏水时间的关系调查研究,在滴水的水龙头下放置一个量筒,每5分钟记录一次水量,如下表.时间
0
5
10
15
20
25
30
水量
0
1.5
3
4.5
6
8.5
9
(1)、兴趣小组通过分析上表中的数据发现漏水量与漏水时间存在一种特殊的函数关系,并发现有一组水量记录错了,上表中记录错误的数值是 , 这个数值修改正确应该是;请你直接写出漏水量 关于漏水时间 的函数关系式;(2)、该学校有6个洗手房,每个洗手房有10个水龙头,假设每个水龙头都没有关严,且每个水龙头滴水速度都与上表中的速度相同,请你估计该学校一天(24小时)的漏水量;关紧一小步,素质一大步,随手关水龙头.或者:不要让水龙头孤独的流泪!!!每个水龙头一天的漏水量 , .
答:该学校一天的漏水量为 (或 )
为了增强学生的节水意识,请你帮兴趣小组写一句提醒学生关紧水龙头的提示语: .
20. 阅读下列材料,完成相应任务.直角三角形斜边上的中线等于斜边的一半
如图1, 中, , 是斜边 上的中线.求证: .
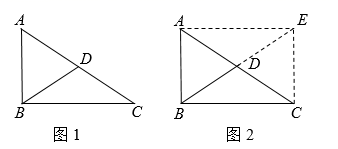
分析:要证明 等于 的一半.可以用“倍长法”将 延长一倍,如图2,延长 到 ,使得 .连接 , .可证四边形 是矩形,由矩形的对角线相等得 ,这样将直角三角形斜边上的中线与斜边的数量关系转化为矩形对角线的数量关系,进而得到 .
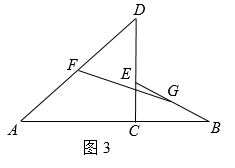 (1)、请你按材料中的分析写出证明过程;(2)、上述证明方法中主要体现的数学思想是______;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、如图3,点 是线段 上一点, ,点 是线段 上一点,分别连接 , ,点 , 分别是 和 的中点,连接 .若 , , .则 .21. 综合与实践.
(1)、请你按材料中的分析写出证明过程;(2)、上述证明方法中主要体现的数学思想是______;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、如图3,点 是线段 上一点, ,点 是线段 上一点,分别连接 , ,点 , 分别是 和 的中点,连接 .若 , , .则 .21. 综合与实践.如图1,将两个全等的三角尺 与三角尺 如图摆放( 与 重合),其中, , .
 (1)、如图2,固定三角尺 不动,将三角尺 沿 方向平移至图2位置,分别连接 , .则四边形 的形状为;(2)、如图3,在图2的基础上,将三角尺 沿 方向继续平移,当四边形 是菱形时,分别连接 , .
(1)、如图2,固定三角尺 不动,将三角尺 沿 方向平移至图2位置,分别连接 , .则四边形 的形状为;(2)、如图3,在图2的基础上,将三角尺 沿 方向继续平移,当四边形 是菱形时,分别连接 , .①请判断此时四边形 的形状,并说明理由;
②若 ,则四边形 的周长为 ▲ .
22. 综合与探究.如图1,直线 与坐标轴交于 , 两点,已知点 的坐标为 ,点 的坐标为 ,点 是线段 上一点.
 (1)、求直线 的解析式;(2)、如图1,设点 的横坐标为 , 的面积为 ,请你用含 的式子表示 ,并求当 的面积等于 面积的 时 的值;(3)、如图2,过点 作线段 的垂线,交 轴于点 ,连接 ,当 时,求点 的坐标.
(1)、求直线 的解析式;(2)、如图1,设点 的横坐标为 , 的面积为 ,请你用含 的式子表示 ,并求当 的面积等于 面积的 时 的值;(3)、如图2,过点 作线段 的垂线,交 轴于点 ,连接 ,当 时,求点 的坐标.