内蒙古自治区包头市青山区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 已知a＜b ，下列式子不一定成立的是（）

A、na＜nb B、﹣2a＞﹣2b C、 $\frac{1}{2}$ a+1＜ $\frac{1}{2}$ b+1 D、a﹣1＜b﹣1

查看试题解析
2. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史． $2017$ 年 $5$ 月，世界围棋冠军柯洁与人工智能机器人 $AlphaGo$ 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）

A、 B、 C、 D、

查看试题解析
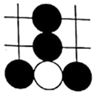3. 在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是( )

A、频率就是概率 B、频率与试验次数无关 C、概率是随机的，与频率无关 D、随着试验次数的增加，频率一般会越来越接近概率

查看试题解析
4. 下列运算中正确的是（）

A、 $\frac{0.2 a + b}{0.7 a - b}$ ＝ $\frac{2 a + b}{7 a - b}$ B、 $\frac{a - b}{b - a} = - 1$ C、 $\frac{- b}{2 a^{2}}$ • $\frac{a}{- b^{2}}$ ＝﹣ $\frac{1}{2 a b}$ D、 $\frac{m}{x} \div \frac{n}{x} = \frac{n}{m}$

查看试题解析
5. 若多边形的边数由n增加到n+1（n为大于3的正整数），则其内角和的度数（）

A、增加180° B、减少180° C、不变 D、不能确定

查看试题解析
6. 如图，平行四边形ABCD中，EF∥BC，GH∥AB，EF，GH相交于点O，则图中有平行四边形（）

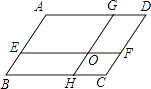A、4个 B、5个 C、8个 D、9个

查看试题解析
7. 如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长是（　　）

A、8 B、10 C、12 D、16

查看试题解析
8. 因式分解 $x^{2} + m x + n$ 时，甲看错了 $m$ 的值，分解的结果是 $(x - 6) (x + 2)$ ，乙看错了 $n$ 的值，分解的结果为 $(x + 8) (x - 4)$ ，那么 $x^{2} + m x + n$ 分解因式正确的结果为（）

A、 $(x + 3) (x - 4)$ B、 $(x + 4) (x - 3)$ C、 $(x + 6) (x - 2)$ D、 $(x + 2) (x - 6)$

查看试题解析
9. 下列命题中，真命题是（）

A、如果把分式 $\frac{x y}{x + y}$ 中的x和y都扩大3倍，那么分式的值也扩大3倍 B、若b＞a＞0，则 $\frac{a}{b} > \frac{a + 1}{b + 1}$ C、对角线相等的四边形是矩形 D、顺次连接菱形四边中点得到的四边形是正方形

查看试题解析
10. 如图，在▱ABCD中，AD＝2AB ， F是AD的中点，作CE⊥AB ，垂足E在线段AB上，连接EF、CF ，下列结论中：①∠DCF＝ $\frac{1}{2}$ ∠BCD；②∠DFE＝3∠AEF；③EF＝CF；④S_△BEC＝S_△CEF ．一定成立的是（）

A、①②③④ B、①②③ C、①②④ D、①③④

查看试题解析

二、填空题

11. 当x=时，分式 $\frac{x^{2} - 9}{x + 3}$ 的值为零.

查看试题解析
12. 已知 $a b = - 4$ ， $a + b = 2$ ，则 $a^{2} b + a b^{2}$ 的值为.

查看试题解析
13. 计算： $\frac{1}{x} \div \frac{x^{2} - 2 x + 1}{x^{2} - x} =$ ．

查看试题解析
14. 如图，在正方形 ABCD ，E是对角线 BD 上一点， AE 的延长线交 CD 于点F ，连接 CE ．若∠BAE=56° ，则 ∠CEF= ° ．

查看试题解析
15. 已知a、b可以取﹣2、﹣1、1、2中任意一个值（a≠b），则直线y=ax+b的图象不经过第四象限的概率是.

查看试题解析
16. 解不等式组 ${\begin{matrix} - 3 x \leq 9 \\ x > - 2 \\ 2 (x + 1) < x + 3 \end{matrix}$ 得．

查看试题解析
17. 如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别为 $S_{1}$ 、 $S_{2}$ ，则 $S_{1}$ 与 $S_{2}$ 的大小关系是．

查看试题解析
18. 如图，在Rt△ABC中，∠ACB＝90°，BC＞AC ，按以下步骤作图：

⑴分别以点A ， B为圆心，以大于 $\frac{1}{2}$ AB的长为半径作弧，两弧相交于M ， N两点（点M在AB的上方）；

⑵作直线MN交AB于点O ，交BC于点D；

⑶用圆规在射线OM上截取OE＝OD ．连接AD ， AE ， BE ，过点O作OF⊥AC ．垂足为F ，交AD于点G ．

下列结论：①CD＝2GF；②BD²﹣CD²＝AC²；③S_△BOE＝2S_△AOG；其中正确的结论有．（填序号）

查看试题解析

三、解答题

19. 解方程： $\frac{x}{x - 1} - \frac{2 x}{3 x - 3} = 1$ ．

查看试题解析
20. 先化简： $\frac{x^{2} - 4}{x^{2} + 4 x + 4} \div (x - 2 - \frac{2 x - 4}{x + 2})$ ，再在﹣2，0，1，2四个数中选一个合适的数作为x的取值代入求值．

查看试题解析
21. 一个不透明的箱子里装有3个红色小球和若干个白色小球，每个小球除颜色外其他完全相同，每次把箱子里的小球摇匀后随机摸出一个小球，记下颜色后再放回箱子里，通过大量重复实验后，发现摸到红色小球的频率稳定于0.75左右.

(1)、请你估计箱子里白色小球的个数；

(2)、现从该箱子里摸出1个小球，记下颜色后放回箱子里，摇匀后，再摸出1个小球，求两次摸出的小球颜色恰好不同的概率（用画树状图或列表的方法）.

查看试题解析
22. 如图，E、F是▱ABCD对角线AC上两点，且AE＝CF．

(1)、求证：四边形BFDE是平行四边形．

(2)、如果把条件AE＝CF改为BE＝DF ，试问四边形BFDE还是平行四边形吗？为什么？

查看试题解析
23. 为应对新冠疫情，某药店到厂家选购A、B两种品牌的医用外科口罩，B品牌口罩每个进价比A品牌口罩每个进价多0.7元，若用7200元购进A品牌数量是用5000元购进B品牌数量的2倍．

(1)、求A、B两种品牌的口罩每个进价分别为多少元？

(2)、若A品牌口罩每个售价为2元，B品牌口罩每个售价为3元，药店老板决定一次性购进A、B两种品牌口罩共6000个，在这批口罩全部出售后所获利润不低于1800元．则最少购进B品牌口罩多少个？

查看试题解析
24. 已知，如图1，BD是边长为1的正方形ABCD的对角线，BE平分∠DBC交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G.

(1)、求证：△BCE≌△DCF；

(2)、求CF的长；

(3)、如图2，在AB上取一点H，且BH=CF，若以BC为x轴，AB为y轴建立直角坐标系，问在直线BD上是否存在点P，使得以B、H、P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的P点坐标；若不存在，说明理由.

查看试题解析