黑龙江省齐齐哈尔市建华区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 的值为( )A、4 B、-2 C、± 2 D、22. 下列各组数据中,可以构成一个直角三角形的三边的是( )A、6、7、8 B、5、12、14 C、6、8、10 D、5、7、93. 下列各点中,不在直线 y = 2x +1上的是( )A、(1,3) B、(0,1) C、(2,4) D、(-1,-1)4. 下列条件中能判断一个四边形是菱形的是( )A、对角线互相平分且相等 B、对角线互相垂直且相等 C、对角线互相平分且垂直 D、对角线互相垂直且一条对角线平分一组对角5. 某青年排球队12名队员的年龄情况如下:
年龄(单位:岁)
18
19
20
21
22
人数
1
4
3
2
2
则这个队队员年龄的众数和中位数是( )
A、 B、 C、 D、6. 如图, 中, , , ,P是对角线AC上任一点(点P不与点A、C重合),且 交AB于E , 且 交AD于F , 则阴影部分的面积为( ) A、5 B、 C、10 D、7. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )
A、5 B、 C、10 D、7. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )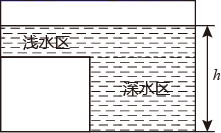 A、
A、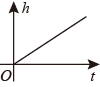 B、
B、 C、
C、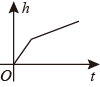 D、
D、 8. 在 Rt△ABC 中,∠B=90°,BC=15,AC=17,以 AB 为直径作半圆,则此半圆的面积( )A、 B、 C、 D、9. 如图,矩形 ABCD 中,对角线 AC 与 BD 交于点 O , AB=3, BC=4,点 P 为边 AD 上的动点,PE⊥AC 于点 E , PF⊥BD 于点 F , 则 PE+PF 的值为( )
8. 在 Rt△ABC 中,∠B=90°,BC=15,AC=17,以 AB 为直径作半圆,则此半圆的面积( )A、 B、 C、 D、9. 如图,矩形 ABCD 中,对角线 AC 与 BD 交于点 O , AB=3, BC=4,点 P 为边 AD 上的动点,PE⊥AC 于点 E , PF⊥BD 于点 F , 则 PE+PF 的值为( )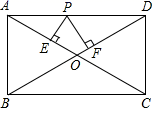 A、 B、 C、5 D、710. 已知,从-3、-2 、-1、1、2、3 六个数中任取一个数记为 k , 如果数 k 使得关于 x的分式方程 有解,且使关于x 的一次函数 y = (k + )x +1 不经过第四象限,那么这六个数中,所有满足条件的 k 值的个数为( )A、1 B、2 C、3 D、4
A、 B、 C、5 D、710. 已知,从-3、-2 、-1、1、2、3 六个数中任取一个数记为 k , 如果数 k 使得关于 x的分式方程 有解,且使关于x 的一次函数 y = (k + )x +1 不经过第四象限,那么这六个数中,所有满足条件的 k 值的个数为( )A、1 B、2 C、3 D、4二、填空题
-
11. 计算 = .12. Rt△ABC 中,∠C=90°,∠A=45°,AC= ,则 AB= .13. 某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此实际平均数与求出的平均数的差为 .14. 若0≤a≤3 ,则 = .15. 矩形 ABCD 的一组邻边分别为 1 和 4,若点 E 为边 AD 上一点, 且 AE= ,则EC= .16. 如果一次函数 y = ax + 4 与 y = bx - 2 的图象的交点在 x 轴上,那么经过点(1,1)的直线 y = x + c 的表达式为 .17. 如图, 正方形 A1B1B2C1 、 A2B2B3C2 、A3B3B4C3、… …按如图所示的方式放置.点 A1 A2、A3、…和点 B1、B2、B3、…分别在直线 y = x和 x 轴上, 若点 B1(1 , 0), 则点 Cn 的坐标是 .

三、解答题
-
18. 计算:(1)、 ;(2)、 .19. 分解因式(在实数范围内): .20. 在平面直角坐标系中,一次函数 y=kx+b(k ≠ 0)的图象由函数 y=x 的图象平移得到, 且经过点 A(1,2).
 (1)、求这个一次函数的解析式;(2)、在所给的平面直角坐标系中画出这个一次函数的图象.若此图象与 x 轴交于点 B , 则△ABO 的面积为 .(3)、当 x>1 时,对于每一个 x 的值,函数 y=mx(m≠0)的值都大于一次函数 y=kx+b 的值,请你直接写出 m 的取值范围: .21. 为调动学生参加“阳光体育”活动的积极性,某校初二进行踢毽子比赛,每班选派 5 名学生参加,按团体总分的多少排列名次,在规定时间内每人踢 100 个以上(含 100)为优秀,下表是成绩最好的 A 班和 B 班各 5 名学生的比赛数据(单位:个):
(1)、求这个一次函数的解析式;(2)、在所给的平面直角坐标系中画出这个一次函数的图象.若此图象与 x 轴交于点 B , 则△ABO 的面积为 .(3)、当 x>1 时,对于每一个 x 的值,函数 y=mx(m≠0)的值都大于一次函数 y=kx+b 的值,请你直接写出 m 的取值范围: .21. 为调动学生参加“阳光体育”活动的积极性,某校初二进行踢毽子比赛,每班选派 5 名学生参加,按团体总分的多少排列名次,在规定时间内每人踢 100 个以上(含 100)为优秀,下表是成绩最好的 A 班和 B 班各 5 名学生的比赛数据(单位:个):1 号
2 号
3 号
4 号
5 号
总数
A 班
100
95
110
91
104
500
B 班
89
100
96
118
97
500
经统计发现两班的总数相同.有同学建议可考查数据中的其它信息确定优胜班级.请你回答下列问题:
(1)、计算两班的优秀率;(2)、写出两班比赛成绩的中位数;(3)、两班比赛成绩的方差哪一个小?(4)、根据上面信息,你认为应该将优胜奖状颁发给哪个班?简要说明理由.22. 如图,点 O 为菱形 ABCD 对角线 AC、BD 的交点,点 E 为边 BC 的中点,连接 OE , EF⊥DC 于点 F,OG∥EF , OG 交 CD 于点 G .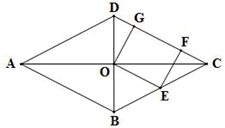 (1)、求证:四边形 OEFG 为矩形;(2)、若 AB=10,EF=4,求 OE 和 DG 的长.23. 综合与实践(1)、动手、发现:
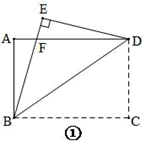
(1)、求证:四边形 OEFG 为矩形;(2)、若 AB=10,EF=4,求 OE 和 DG 的长.23. 综合与实践(1)、动手、发现:数学活动课上,小聪进行了下列操作:“如图①,矩形纸片 ABCD 中,BD 为对角线,将△BCD 沿 BD折叠,使点 C 落在点 E 处,BE 交 AD 于点 F . ”则线段 BF= , △ABF≌△;
 (2)、问题解决:
(2)、问题解决:在图①中,若 AB=6,BC=8,请你求出线段 AF 的长;
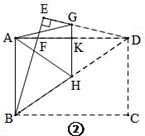
(3)、再动手、延伸:小聪在(2)的条件下,找到 DE 上的点 G 及 BD 上的点 H , 将△GDH 沿 GH 折叠,使点 D 落在点 A 处(如图②), 则线段 GH 的长为: .
 24. 综合与探究
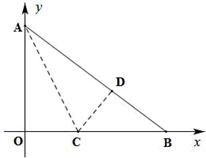
24. 综合与探究如图,点A、点B分别在y轴、 轴的正半轴上, OA:OB=3:4 ,且OA是方程 的根.将△OAB 沿直线AC折叠,使点O落在线段 AB 上的点D处.
 (1)、求 OA、OB 的长;(2)、求点C的坐标;(3)、①若直线l经过点 E(0,-2)且平行于x轴,在直线 l 上找一点G , 使 AG+CG 最短,请你直接写出点 G 的坐标;
(1)、求 OA、OB 的长;(2)、求点C的坐标;(3)、①若直线l经过点 E(0,-2)且平行于x轴,在直线 l 上找一点G , 使 AG+CG 最短,请你直接写出点 G 的坐标;②在 x 轴上是否存在这样的点 M , 使得以点 A、C、M 为顶点的三角形为等腰三角形? 若存在,请直接写出点 M 的坐标;若不存在,请说明理由.