广东省深圳市龙岗区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若实数a，b满足 $a > b$ ，则（）

A、 $a > 2 b$ B、 $2 a > b$ C、 $a + 2 > b + 1$ D、 $a - 2 > b - 1$

查看试题解析
3. 下列各式中，属于因式分解的是（）

A、 $(x + y) (x - 2 y) = x^{2} - x y + y^{2}$ B、 $3 x^{2} - x = x (3 x - 1)$ C、 ${(a - b)}^{2} = (a - b) (a - b)$ D、 $25 {(x - 2 y)}^{2} - 4 {(2 y - x)}^{2}$

查看试题解析
4. 下列各式中，是分式的为（）

A、 $\frac{3}{5}$ （1﹣x） B、 $\frac{x}{3}$ C、 $\frac{3}{x^{2} + 2 y}$ D、1 $- \frac{x}{2}$

查看试题解析
5. 下列用数轴表示不等式组 ${\begin{array}{l} x > 1 \\ x \leq 2 \end{array}$ 的解集正确的是（）

A、 B、 C、 D、

查看试题解析
6. 在以下现象中：①用打气筒打气时，气筒里活塞的运动；②传送带上，瓶装饮料的移动；③在笔直的公路上行驶的汽车；④温度计中，液柱的上升或下降；⑤钟摆的摆动．属于平移的是（）

A、① B、①② C、①②③ D、①②③④

查看试题解析
7. 如图，△ABC中，DE是AC的垂直平分线，AE= 5cm，△ABD的周长为16cm，则△ABC的周长为（）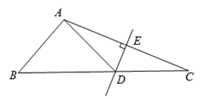

A、21cm B、26cm C、28cm D、31cm

查看试题解析
8. 已知a＜b ，则 ${\begin{array}{l} x < b \\ x > a \end{array}$ 的解集是（）

A、x＜5 B、x＞a C、a＜x＜b D、无解

查看试题解析
9. 若关于x的分式方程 $\frac{a}{x - 3} - \frac{1}{3 - x} = 2$ 有增根，则a的值为（）

A、 $a = 1$ B、 $a = - 1$ C、 $a = 3$ D、 $a = - 3$

查看试题解析
10. 如图在 $▱ A B C D$ 中， $∠ A B C = 60^{\circ} ， B C = 2 A B = 8$ ，点C关于 $A D$ 的对称点为E ，连接 $B E$ 交 $A D$ 于点F ，点G为 $C D$ 的中点，连接 $E G$ ， $B G$ ．则 $△ B E G$ 的面积为（）

A、 $16 \sqrt{3}$ B、 $14 \sqrt{3}$ C、 $8 \sqrt{3}$ D、 $7 \sqrt{3}$

查看试题解析

二、填空题

11. 要使分式 $\frac{3}{x + 1}$ 有意义，则实数 $x$ 的取值范围是．

查看试题解析
12. 分解因式： $a^{2} - 4 b^{2} =$ ．

查看试题解析
13. 正八边形的每个外角为度．

查看试题解析
14. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象如图所示，那么关于x的不等式 $k x + b > 0$ 的解集是．

查看试题解析
15. 如图，等腰△ABC中， $∠ B A C = 150 °$ ，D是AB上一点， $A D = 1$ ， $B D = 4$ ，E点在边BC上，若点E绕点D逆时针旋转 $15 °$ 的对应点F恰好在AC上，则BE的长度为．

查看试题解析

三、解答题

16.

(1)、解不等式组： ${\begin{matrix} 3 x - 5 \leq 1 \\ \frac{13 - x}{3} < 4 x \end{matrix}$ ；

(2)、分解因式： ${(x - y)}^{3} - 9 (x - y)$ ．

查看试题解析
17. 先化简，再求值： $(1 - \frac{2}{x + 1}) \div \frac{x - 1}{x^{2} + 2 x + 1}$ ，其中 $x = \sqrt{3} - 1$ ．

查看试题解析
18. 解方程： $\frac{3}{x - 3} = 1 - \frac{3 x}{3 - x}$ ．

查看试题解析
19. 某种型号油电混合动力汽车，从A地到B地燃油行驶需纯燃油费用76元，从A地到B地用电行驶需纯用电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元．

(1)、求每行驶1千米纯用电的费用；

(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元，则至少需用电行驶多少千米？

查看试题解析
20. 如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE．

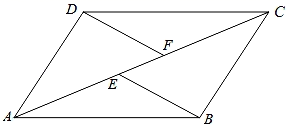(1)、求证：四边形ABCD是平行四边形；

(2)、若∠CEB＝2∠EBA，BE＝3，EF＝2，求AC的长．

查看试题解析
21. 如图，已知 $A (8 ， 0)$ ，P是y轴上一动点，线段PA绕着点P按逆时针方向旋转 $90 °$ 至线段PB位置，连接AB、OB ．

(1)、设P点坐标为 $(0 ， m)$ ，请求出B点坐标；

(2)、求BO+BA的最小值．

查看试题解析
22. 如图，已知∠AOB＝60°，在∠AOB的平分线OM上有一点C，∠DCE＝120°，当∠DCE的顶点与点C重合，它的两条边分别与直线OA、OB相交于点D、E．

(1)、当∠DCE绕点C旋转到CD与OA垂直时（如图1），请猜想OE+OD与OC的数量关系，并说明理由；

(2)、由（图1）的位置将∠DCE绕点C逆时针旋转θ角（0＜θ＜90°），线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，并说明理由．

查看试题解析