广东省深圳市宝安区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{1}{x - 4}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \neq 4$ B、 $x \neq - 4$ C、 $x > 4$ D、 $x > - 4$

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 不等式 $x - 6 < 2 x$ 的解集为（）

A、 $x < 6$ B、 $x > - 6$ C、 $x > 2$ D、 $x < 2$

查看试题解析
4. 下列各式中，从左到右是因式分解的是（）

A、 $a x + a y + a = a (x + y)$ B、 $t^{2} - 4 + 3 t = (t + 2) (t - 2) + 3$ C、 $y^{2} + 4 y + 4 = {(y + 2)}^{2}$ D、 ${(a - b)}^{2} = a^{2} - b^{2}$

查看试题解析
5. 下列分式运算中正确的是（）

A、 $\frac{1}{a} + \frac{1}{b} = \frac{1}{a + b}$ B、 $\frac{a}{b} = \frac{a + 1}{b + 1}$ C、 $\frac{a + b}{a^{2} + b^{2}} = \frac{1}{a + b}$ D、 $\frac{a}{b} \div \frac{d}{c} = \frac{a c}{b d}$

查看试题解析
6. 如图，在平行四边形 $A B C D$ 中，分别以 $A$ 、 $C$ 为圆心，大于 $\frac{1}{2} A C$ 的长为半径画弧，两弧分别交于 $G$ 、 $H$ 两点，分别交 $A D$ 、 $A C$ 、 $B C$ 分别于点 $E$ 、 $O$ 、 $F$ ，已知 $△ D C E$ 的周长为12，则平行四边形 $A B C D$ 的周长为（）

A、12 B、18 C、20 D、24

查看试题解析
7. 下列命题正确的是（）

A、两边分别相等的两个直角三角形全等 B、正八边形的每个外角都等于45° C、对角线相等的四边形是平行四边形 D、 $P (a ， b)$ 关于原点对称的点的坐标为 $(- b ， - a)$

查看试题解析
8. 如图，已知 $△ A B C$ 是等腰直角三角形， $∠ A C B = 90 °$ ， $A B =2$ ，将 $△ A B C$ 沿直线 $A B$ 平移到 $△ D E F$ 的位置，当 $D$ 恰好是 $A B$ 中点时，则AE的长（）

A、 $\sqrt{5}$ B、2 C、 $2 \sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
9. “六一八”购物狂欢节来临之际，某电商平台为了扩大销量，决定打折促销，已知某款音响的进价为600元，标价为900元，要保持获利不低于5%，则该电商平台至多可以打（）销售．

A、九五折 B、八折 C、七五折 D、七折

查看试题解析
10. 如图，将两个全等的等腰直角三角形摆成如图所示的样子，其中 $A B = A C = A G = F G$ ， $A F$ 、 $A G$ 分别与 $B C$ 交于 $D$ 、 $E$ 两点，将 $△ A C E$ 绕着点 $A$ 顺时针旋转90°得到 $△ A B H$ ；① $B H ⊥ B C$ ，② $A D$ 平分 $∠ H D E$ ；③若 $B D = 3$ ，CE=4，则 $A B = 6 \sqrt{2}$ ；④若 $A B = B E {， S}_{△ A B D} = \frac{1}{2} S_{△ A D E}$ ，其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解： $2 m n^{2} - 12 m n + 18 m =$ ．

查看试题解析
12. 定义新运算： $a # b = \frac{1}{b^{2} - a b}$ ，例如 $2 # 3 = \frac{1}{3^{2} - 3 \times 2} = \frac{1}{3}$ ，则方程 $x # 2 = 1$ 的解为．

查看试题解析
13. 如图，一次函数 $y = k x + b$ 与正比例函数 $y = - 2 x$ 交于 $B (m ， 2)$ ，则关于 $x$ 的不等式 $k x + b \leq - 2 x$ 的解集为．

查看试题解析
14. 如图，平行四边形 $A B C D$ ， $∠ A B C$ 和 $∠ B C D$ 的平分线交于点 $E$ ，过点E作EF∥AB交BC于F ，连接 $A E$ 并延长交 $C D$ 于 $G$ ，若 $A B = 5$ ，BC=6，则线段 $D G$ 的长为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ C A B = 60 °$ ， $A B = 10$ ， $A C = 6$ ，将线段 $B C$ 绕着点 $B$ 逆时针旋转60°得到 $A C^{'}$ ， $C C^{'}$ ，则 $△ A B C^{'}$ 的面积为．

查看试题解析
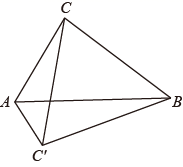16. 如图，在长度均为1的正方形网格中建立如图所示的平面直角坐标系，已知 $A (1 ， 0)$ ， $B (4 ， 2)$ ， $C (2 ， 4)$ ．

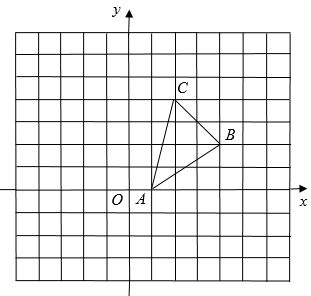(1)、将 $△ A B C$ 沿着 $x$ 轴向左平移5个单位后得到 $△ A^{'} B^{'} C^{'}$ ，请在图中画出平移后 $△ A^{'} B^{'} C^{'}$ ，则 $C$ 的对应点 $C^{'}$ 的坐标为 ▲ ．

(2)、线段 $A^{'} B^{'}$ 可以看成是线段 $B A$ 绕着某个定点旋转180°后得到的图形，这个定点的坐标是．

(3)、若 $P$ 是 $y$ 轴上的一个动点，连接 $P B$ 、 $P C$ ，则 $| P B - P C |$ 的最大值为．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 3 (x - 1) < 2 x + 1 \\ \frac{x - 1}{2} + 1 \geq \frac{1}{3} x \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
18. 先化简 $(\frac{x + 1}{x^{2} - 2 x + 1} + \frac{1}{x + 1}) \div \frac{2 x}{x^{2} - 1}$ ，然后从－1，0，1，2中选取一个你认为合适的数作为 $x$ 的值代入求值．

查看试题解析
19. 解方程： $\frac{x - 1}{2 x - 3} = 1 - \frac{1}{3 - 2 x}$ ．

查看试题解析
20. 如图， $△ A B C$ 为直角三角形， $∠ A C B = 90 °$ ， $B E ⊥ B C$ ， $F$ 是 $A B$ 中点， $D$ 为边 $A C$ 上的一个动点（不与 $A$ ， $C$ 重合），连接 $D F$ ，连接 $A E$ ， $B D$ ．

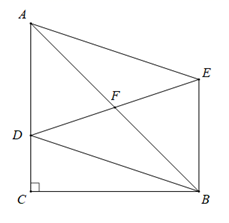(1)、求证：四边形 $A D B E$ 为平行四边形；

(2)、若 $A C = 8$ ， $B C = 6$ ， $A D = B D$ ，求EF、DE ．

查看试题解析
21. 端午节是我国传统节日，粽子是端午节必不可少的美食，某超市在端午节来临前夕，经过市场调研， $A$ ， $B$ 两种品牌粽子销售较好，B种品牌粽子比A种品牌粽子贵2元，用960元购买 $A$ 种粽子的数量是用720元购买 $B$ 种粽子数量的2倍．

(1)、求 $A$ 、 $B$ 两种品牌粽子每个的进价分别为多少元？

(2)、若该超市将 $A$ 种品牌粽子的售价定为6元， $B$ 种品牌粽子的售价定为10元，超市准备用3200元购进 $A$ 、 $B$ 两种品牌的粽子进行销售， $A$ 种品牌粽子打9折销售， $B$ 种品牌粽子降价2元，总利润不低于1080元，那么至少应购进 $A$ 种品牌粽子多少个．

查看试题解析
22. 如图1，直线 $y = - \frac{4}{3} x + 4$ 与 $x$ 、 $y$ 轴分别交于 $A$ ，以 $A B$ 为直角边在第一象限内作等腰直角△ABC ， $∠ B A C = 90 °$

(1)、 $C$ 点坐标为；

(2)、如图2，点 $E$ 为线段 $O B$ 上的一个动点（ $E$ 不与 $B$ 、 $O$ 重合），连接 $A E$ ，以 $A E$ 为直角边作等腰直角△AEF ，连接 $C F$ 交 $x$ 轴于 $G$ ，求证： $G$ 是 $F C$ 的中点；

(3)、如图3，将 $△ A B C$ 沿着 $x$ 轴向左平移得到 $△ A^{'} B^{'} C^{'}$ ，直线 $A^{'} B^{'}$ 与 $y$ 轴交于点 $M$ ，若以 $A ， B ， M$ 为顶点的三角形是等腰三角形，请求出点 $A^{'}$ 的坐标．

查看试题解析