广东省汕尾市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围是（）

A、 $x \geq - 2$ B、 $x > - 2$ C、 $x \geq 2$ D、 $x > 2$

查看试题解析
2. 根据全国第七次人口普查统计公报的数据显示：汕尾市常住人口为2672819人，其中2672819用科学记数法表示为（）

A、 $26.72819 \times 10^{5}$ B、 $2.672819 \times 10^{5}$ C、 $2.672819 \times 10^{6}$ D、 $0.2672819 \times 10^{7}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{5}$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 ${(x y)}^{2} = x y^{2}$ D、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$

查看试题解析
4. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ，以点A为圆心，AC长为半径画弧，交AB于点D ，则BD的长度是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列各式中是最简二次根式的是（）

A、 $\sqrt{\frac{1}{5}}$ B、 $\sqrt{15}$ C、 $\sqrt{0.1}$ D、 $\sqrt{8}$

查看试题解析
6. 下列四点在函数 $y = 3 x + 2$ 的图象上的点是（）

A、 $(- 1 ， 1)$ B、 $(0 ， - 1.5)$ C、 $(2 ， 0)$ D、 $(- 1 ， - 1)$

查看试题解析
7. 根据疫情防控要求，所有乘坐高铁的乘客都须测量体温，在某个时间段有7名乘客的体温（单位：℃）如下：36.5，36.3，36.8，36.3，36.5，36.7，36.5，这7名乘客体温的众数是（）

A、36.3 B、36.8 C、36.5 D、36.7

查看试题解析
8. 在平行四边形ABCD中，下列结论中，错误的是（）

A、 $A B = C D$ B、 $A C = B D$ C、当 $A C ⊥ B D$ 时，平行四边形ABCD是菱形 D、当 $∠ A B C = 90 °$ ，平行四边形ABCD是矩形

查看试题解析
9. 某服装加工厂加工校服960套的订单，原计划每天做48套．正好按时完成．后因学校要求提前5天交货，为按时完成订单，设每天就多做x套，则x应满足的方程为（）

A、 $\frac{960}{48 + x} - \frac{960}{48} = 5$ B、 $\frac{960}{48} + 5 = \frac{960}{48 + x}$ C、 $\frac{960}{48} - \frac{960}{x} = 5$ D、 $\frac{960}{48} - \frac{960}{48 + x} = 5$

查看试题解析
10. 如图，点P从正方形ABCD的顶点C出发，沿着正方形的边运动，依次经过点D和点A ，到达点B后停止运动．当运动路程为x时， $△ P B C$ 的面积为y ，则y随x变化的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 分解因式： $a^{2} - 4 =$ .

查看试题解析
12. 某校甲乙两支篮球队队员的平均身高相等，甲队队员身高的方差 $S_{甲}^{2} = 1.9$ ，乙队队员身高的方差 $S_{乙}^{2} = 1.6$ ，那么两队中身高更整齐的是队．

查看试题解析
13. 已知一次函数 $y = (k - 2) x + 3$ ，若y值随x值的增大而减少，则k的取值范围是．

查看试题解析
14. 若菱形的两条对角线长分别是8cm和10cm，则该菱形的面积是 ${cm}^{2}$ ．

查看试题解析
15. 将正比例函数 $y = 3 x$ 的图象沿y轴向下平移2个单位后所得图象的解析式是．

查看试题解析
16. 如图将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F处，已知CE=3，AB=8，则BF= .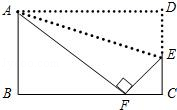

查看试题解析
17. 如图，已知 $△ A B C$ 是腰长为1的等腰直角三角形，以 $Rt △ A B C$ 的斜边AC为直角边，画第二个等腰 $Rt △ A C D$ ，再以 $Rt △ A C D$ 的斜边AD为直角边，画第三个等腰 $Rt △ A D E$ ，……依此类推，则第2021个等腰直角三角形的斜边长是．

查看试题解析

三、解答题

18. $2^{- 1} + | \sqrt{3} - 1 | + 2021^{0} - \frac{1}{2} \sqrt{12}$ ．

查看试题解析
19. 先化简，再求值： $(\frac{2}{x - 1} + \frac{1}{x + 1}) \cdot (x^{2} - 1)$ ，其中 $x = \frac{\sqrt{3}}{3}$ ．

查看试题解析
20. 如图，BD是平行四边形ABCD的对角线， $∠ C = 30 °$ ，

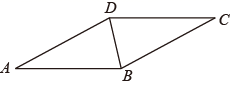(1)、请用尺规作图法，作AB的垂直平分线EF ，垂足为E ，交AD于F；（不要求写作法，保留作图痕迹）

(2)、在（1）条件下，连接BF ，求 $∠ D F B$ 的度数．

查看试题解析
21. 今年3月22日“世界水日”，红星中学数学活动小组到某住宅区调查了解住宅区去年用水情况．该数学活动小组从住宅区中随机抽样调查了50个家庭去年每个月的用水情况，根据调查数据得到下面两张统计图：图1是去年50个家庭的月总用水量折线统计图，图2是去年50个家庭月总用水量的频数分布直方图（不完整）．请根据下面统计图，回答下面问题：

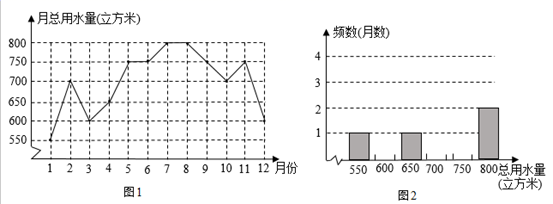(1)、根据图1的信息，补全频数分布直方图（图2）；

(2)、去年50个家庭的月总用水量中，极差是立方米，中位数是立方米；

(3)、根据上面数据，估计去年该住宅区每个家庭平均每月的用水量是多少立方米？

查看试题解析
22. 如图，D、E、F分别是 $△ A B C$ 各边的中点，

(1)、如果 $B C = 8 cm$ ，那么 $E F =$ $cm$ ；

(2)、当AB和AC满足 ▲ 时，四边形AFDE是菱形，并证明．

查看试题解析
23. 为绿化校园，某校计划购进A、B两种树苗，共21棵.已知A种树苗每棵90元，B种树苗每棵70元.设购买B种树苗x棵，够买两种树苗所需费用为y元.

(1)、y与x的函数关系式为：；

(2)、若购买B种树苗的数量少于A种树苗的数量，请给出一种费用最省的方案.并求出该方案所需费用.

查看试题解析
24. 已知一次函数y=kx+b的图象过P（1，4），Q（4，1）两点，且与x轴交于A点．

(1)、求此一次函数的解析式；

(2)、求△POQ的面积；

(3)、已知点M在x轴上，若使MP+MQ的值最小，求点M的坐标及MP+MQ的最小值．

查看试题解析
25. 如图，矩形ABCD中，E是AD的中点，将 $△ A B E$ 沿BE折叠，点A的对应点为点G ．

(1)、填空：如图1，当点G恰好落在BC边上时，四边形ABGE的形状是；

(2)、如图2，当点G落在矩形ABCD内部时，延长BG交DC边于点F ．连接EF ．
①证明： $△ E D F ≌ △ E G F$

②若 $A D = \sqrt{3} A B$ ，试探索线段CD与DF的数量关系．

查看试题解析