广东省汕头市金平区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 下列根式中能与 合并的是( )A、 B、 C、 D、2. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各组线段中,能构成直角三角形的是( )A、2,3,4 B、3,4,6 C、5,12,13 D、4,6,74. 小王和小李两名同学研究本班女同学的身高情况,两人分别统计了一组数据,经过计算得到两组数据的方差,小王一组的方差为1.5,小李一组的方差为2.5;则下列说法正确的是( )
小王
163
164
164
165
165
166
166
167
小李
161
162
164
165
166
166
168
168
A、小王统计的一组数据比较稳定 B、小李统计的一组数据比较稳定 C、两组数据一样稳定 D、不能比较稳定性5. 在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )A、(2,0) B、(-2,0) C、(6,0) D、(-6,0)6. 如图,每个小正方形的边长为1个单位长度,图中阴影部分是正方形,则此正方形的边长为( ) A、 B、 C、 D、7. 大伯出去散步,从家走了20分钟,到一个离家 米的阅报亭,看了10分钟报纸后,用了15分钟返回到家,下面哪个图形表示张大伯离家时间与距离之间的关系( )A、
A、 B、 C、 D、7. 大伯出去散步,从家走了20分钟,到一个离家 米的阅报亭,看了10分钟报纸后,用了15分钟返回到家,下面哪个图形表示张大伯离家时间与距离之间的关系( )A、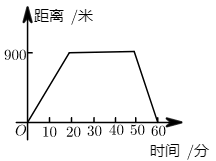 B、
B、 C、
C、 D、
D、 8. 某次射击训练中,以小组的成绩如表所示:已知该小组的平均成绩为8.1环,那么成绩为8环的人数是( )
8. 某次射击训练中,以小组的成绩如表所示:已知该小组的平均成绩为8.1环,那么成绩为8环的人数是( )环数
7
8
9
人数
2
3
A、4人 B、5人 C、6人 D、8人9. 如图,点 是矩形 的中心, 是 上的点,沿 折叠后,点 恰好与点 重合,若 ,则折痕 的长为( )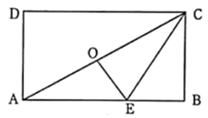 A、 B、 C、 D、10. 如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
A、 B、 C、 D、10. 如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( ) A、
A、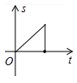 B、
B、 C、
C、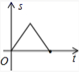 D、
D、
二、填空题
-
11. 若二次根式 有意义,则x的取值范围是 .12. 若点P(3,2)在函数y=3x-b的图像上,则b=.13. 若一组数据 , , , , , 则这组数据的众数是 .14. 如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为 .
 15. 直线y=-2x-6与两坐标轴围成的三角形的面积为.16. 如图,已知 的两条直角边长分别为6、8,分别以它的三边为直径向上作三个半圆,求图中阴影部分的面积为 .
15. 直线y=-2x-6与两坐标轴围成的三角形的面积为.16. 如图,已知 的两条直角边长分别为6、8,分别以它的三边为直径向上作三个半圆,求图中阴影部分的面积为 . 17. 如图,已知直线 的解析式为 ,在点 作 轴的垂直交直线 于点 ,以 为边作第1个正在方形 , 在 轴上, 的延长线交直线 于点 ,以 为边作第2个正在方形 ,……;按此作法继续下去,则第2021个正在方形 的边长 为 .
17. 如图,已知直线 的解析式为 ,在点 作 轴的垂直交直线 于点 ,以 为边作第1个正在方形 , 在 轴上, 的延长线交直线 于点 ,以 为边作第2个正在方形 ,……;按此作法继续下去,则第2021个正在方形 的边长 为 .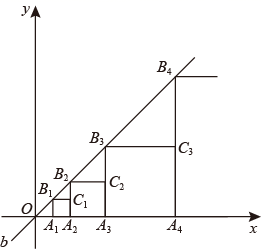
三、解答题
-
18. 计算: .19. 在 中, .
 (1)、作 的垂直平分线,垂足为点 ,与 交于 点(不写作法,保留作图痕迹);(2)、若 , ,连接 ,则 , .20. 如图,在 中, 于 , 于 , .
(1)、作 的垂直平分线,垂足为点 ,与 交于 点(不写作法,保留作图痕迹);(2)、若 , ,连接 ,则 , .20. 如图,在 中, 于 , 于 , . (1)、求证: ;(2)、求 的度数.21. 先化简,再求值: ,其中x= ﹣1.22. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 (千米)与行驶时间 (小时)之间的函数关系如图所示,已知甲对应的函数关系式为 ,根据图象提供的信息,解决下列问题:
(1)、求证: ;(2)、求 的度数.21. 先化简,再求值: ,其中x= ﹣1.22. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 (千米)与行驶时间 (小时)之间的函数关系如图所示,已知甲对应的函数关系式为 ,根据图象提供的信息,解决下列问题: (1)、求乙离开 城的距离 与 的关系式.(2)、求乙出发后几小时追上甲车?23. 中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
(1)、求乙离开 城的距离 与 的关系式.(2)、求乙出发后几小时追上甲车?23. 中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
 (1)、本次抽样调查共抽取了名学生,所得数据的中位数是部;(2)、读完了 部的学生有 ▲ 名,将条形统计图补充完整;(3)、计算该校抽取的这部分学生平均每人看“四大古典名著”多少部?
(1)、本次抽样调查共抽取了名学生,所得数据的中位数是部;(2)、读完了 部的学生有 ▲ 名,将条形统计图补充完整;(3)、计算该校抽取的这部分学生平均每人看“四大古典名著”多少部?

